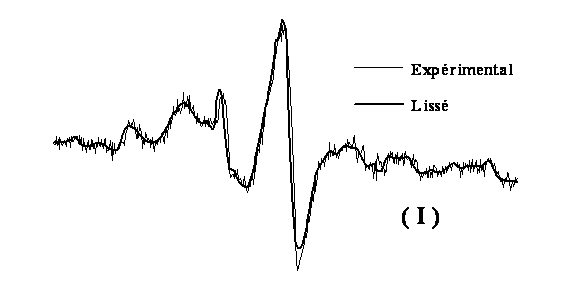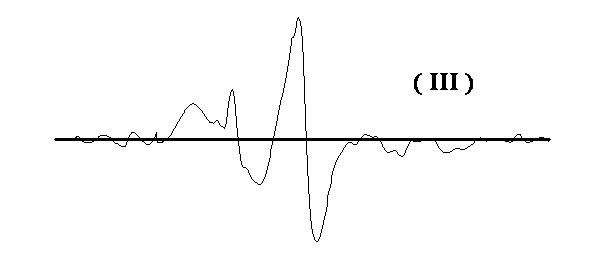TRAITEMENT APL DU SIGNAL.
APPLICATION A
Claude Chachaty
claude.chachaty@wanadoo.fr
Dans le contexte de cet article nous entendons par signal, une grandeur physique
observable dans un domaine limité de temps ou de fréquences, qui se distingue d'une manière
significative du bruit de fond propre au système de détection utilisé. Ce qui
ne fait pas partie du signal est appelé
ligne de base. Pour être identifié et analysé, le signal enregistré sous
forme analogique est numérisé et conservé dans la mémoire d'un ordinateur. On
peut ensuite filtrer le bruit de fond, éliminer les distorsions éventuelles,
puis analyser et si possible interpréter
le signal
.
I - Amélioration du rapport signal/bruit
La transformée de Fourier (T.F.) est souvent employée en spectroscopie pour
améliorer le rapport signal-sur-bruit et pour passer d'un domaine de temps à un
domaine de fréquences et vice-versa.
La relation
entre un signal F() fonction de
la fréquence et sa T.F.
f(t) fonction du temps t est :
![]() [ 1 ]
[ 1 ]
Le signal f(t) est généralement appelé
"interférogramme" ou plus spécifiquement "signal de précession libre" en
résonance magnétique. Le filtrage du bruit s'effectue en multipliant la
fonction f(t) par une fonction w(t) (filtre) qui annule ou réduit le bruit dans
la partie de l'interférogramme où le signal devient négligeable et en
effectuant la transformée de Fourier inverse :
![]() [ 2
]
[ 2
]
La fonction TRANSFO
qui effectue ces opérations, utilise les filtres usuels :
rectangulaire
, exponentiel ou gaussien.
TRANSFO
'Vecteur ou tableau XY0 à transformer' DIM01½VEC0XY0
(2=½½XY0)/'VEC0XY0[;2]'
©
©
--- Compléter le nombre de points à une puissance entière © de 2:
©
DIM1„1†(DIM0ˆ2*¼13)/2*¼13
'Nombre
de points : ',DIM„½VEC„VEC0,((DIM1-DIM0)½0)
'Spectre
XY1' ª PLOT XY1„(¼DIM),[1.5]rDV„VEC
RFFT ª
'Transformée de Fourier : TFV0'
PLOT
(¼0.5×DIM),[1.5](0.5×DIM)†TFV0„rDV
L0:'Filtre rectangulaire [1], exponentiel [2] ou' 'gaussien [3] ? '
…(Ÿ/2
3=CHX„Œ)/L2
©
L1:'Nombre
de points significatifs de TFV0' ª NPTS„Œ
WT„WT,²WT„(NPTS½1),((.5×DIM)-NPTS)½0
ª …L3
©
L2:'Paramètre
de convolution (‘L) ' ª ‘L„Œ
ARG„‘L×¼0.5×DIM ª
–(CHX=3)/'ARG„0.5×ARG×ARG'
WT„WT,²WT„*-ARG
©
L3:iDV„0×rDV„TFV1„TFV0×WT ª 'TFV0×WT =
TFV1'
PLOT (¼0.5×DIM),[1.5](0.5×DIM)†TFV1
IFFT ª XY2„((-DIM0),2)†(¼DIM),[1.5]rDV
–(2=½½XY0)/'XY2„XY0[;1],[1.5]XY2[;2]'
'' ª
'Spectre lissé : XY2 ' ª '' ª PLOT XY2,VEC0
'Correct ? [1]'ª …(1¬Œ)/L0
'Nom attribué à XY2: ' ª
–,'„','XY2'
Les
fonctions RFFT et IFFT existent dans la zone FFT
d'APL+WIN. La fonction RFFT effectue
Le
filtre rectangulaire modifie peu la forme de F(), les filtres exponentiel et gaussien donnent par
contre un spectre moins résolu que
F().
![]() , celle d'une Gaussienne
, celle d'une Gaussienne ![]() est
est
![]() .
.
Pour
effectuer une convolution Lorentzienne ou Gaussienne de F(), il n'est pas indispensable d'utiliser
G F+.(X*2)+(X °. - X)*2 ou G F+.* - ((X °. - X)*2)2X*2
où
X est la demi-largeur
à mi-hauteur de
La
fonction LISSAGE permet d'éliminer
le bruit ("gazon") de densité très supérieure au signal à extraire
sans utiliser
LISSAGE
'Nom du
spectre (dim=2*N) :' ª dim0„1†½XY0„Œ
X0„XY0[;1]
ª 'Facteur de lissage (fac=2*n, n<<N): '
mat„(¼fac)°.=¼fac„Œ
©
© --- réduction du nombre de points
©
i„1 ª xy„(dim0½mat[1;])šXY0
:while i<fac
xy„xy,(dim0½mat[i„i+1;])šXY0
:endwhile
©
© --- Moyenne des spectres réduits:
©
xm„+/((2×fac)½1 0)/xy ª ym„+/((2×fac)½0 1)/xy
©
© --- Interpolation par la méthode de Gauss
©
PLOT
XY1„(2µfac) interpoler (xm,[1.5]ym)÷fac
'Nom
attribué au spectre lissé : ' ª –,'„','XY1'
|
|
Figure 1. (1)
signal F() non traité, (2) interférogramme f(t) obtenu par T.F.
de (1), (3) produit de f(t) par
un filtre rectangulaire w(t), (4)
signal G() obtenu par T.F. de (3).
II
- Correction de la ligne de base.
La
fonction RECTIFIER est destinée à
éliminer la dérive et les distorsions de la ligne de base. Elle fait appel à la
fonction APLANIR pour réduire les
ondulations résiduelles de la ligne de base et les pics parasites. Pour faire
ces corrections on prélève deux segments de ligne de base de part et
d'autre du signal à traiter (AB et CD de la figure 2-II), ajuste à ces deux
segments un polynôme, généralement de degré 4 par les moindres carrés, calcule
les toutes les valeurs du polynôme entre A et D. La courbe AD est soustraite
globalement du signal de façon à supprimer la distorsion de ligne de base. La
fonction RECTIFIER est spécialement
conçue pour traiter les spectres de résonance paramagnétique électronique (RPE)
dont cette figure donne un exemple. Ces
spectres sont le plus souvent enregistrés sous forme de dérivée d'absorption en
fonction d'un champ magnétique croissant linéairement (voir réf. [1]);
cependant la correction de ligne de base est effectuée sur la courbe d'absorption elle même après lissage, correction sommaire de la ligne de
base et intégration de la dérivée.
RECTIFIER
'Nom du
spectre (dérivée d''absorption): '
XY0„Œ
ª X0„XY0[;1]
©
©
--- correction préliminaire de la ligne de base:
©
XY0[;2]„XY0[;2]-0.5×XY0[1;2]+¯1†XY0[;2]
TAB„X0,[1.5]+\XY0[;2]
NPT„10
ª DIF„+/(((-NPT)†TAB[;2])-NPT†TAB[;2])÷NPT
Y1„TAB[1;1]-TAB[;1]
IXY„X0,[1.5]TAB[;2]+DIF×Y1÷(¯1†TAB[;1])-TAB[1;1]
PLOT
TAB,IXY[;2]
©
©
--- Correction de la ligne de base par ajustement polynômial
©
L1:'Nombre de points selectionnés à bas et hauts' 'champs'
(PTS1 PTS2)„Œ ª
IXY2„(PTS1,2)†IXY
IXY3„((-PTS2),2)†IXY
PLOT (PTS1,0)‡(-(PTS2),0)‡DERIV IXY
'Correct ? [1]' ª …(1¬Œ)/L1 ª
IXY1„IXY2®IXY3
'Degré du
polynôme de fit?: '
©
L2:VEC„IXY1[;2]ŽIXY1[;1]°.*0,¼N„Œ
IXY2„IXY1[;1],[1.5](IXY1[;1]°.*0,¼N)+.×VEC
IXY3„(X0°.*0,¼N)+.×VEC
PLOT
IXY„X0,[1.5]IXY[;2]-IXY3
©
© --- Réduire les ondulations de la ligne de base par
© soustraction d'un polynôme de degré n
©
n„7
ª PLOT XY„(n PTS1 PTS2) APLANIR DERIV IXY
IXY„X0,[1.5]+\XY[;2]„XY[;2]÷+/+\XY[;2]
©normaliser
'Spectre
normalisé : XY, intégrale : IXY'
|
|
|
|
|
|
Figure 2. Traitement d'un signal de résonance paramagnétque
électronique (RPE) par les fonctions LISSAGE
(I), RECTIFIER (II). Spectre corrigé
(III).
III - Analyse spectrale.
Après avoir corrigé le signal par les méthodes
exposées plus haut, on procède à une
analyse pour déterminer les positions, les largeurs et les intensités
intégrées (surfaces) des raies qui le composent. On considère généralement en
spectroscopie que les formes des raies élémentaires sont Lorentziennes ou
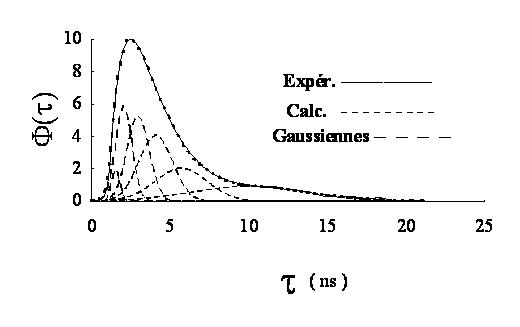
Gaussiennes. A titre d'exemple, la figure 3 montre comment un spectre continu
peut être simulé par une somme de Gaussiennes, à l'aide de la fonction FITGS.
|
|
Figure 3. Décomposition en Gaussiennes élémentaires d'une
distribution de temps de corrélation de réorientation d'un radical nitroxyde
dans le polypropylène solide, déduite d'expériences de résonance paramagnétique
électronique. Cette étude, effectuée en collaboration avec M. Catoire de
lENSAM Paris est destinée à évaluer lhétérogenéité de ce polymère à léchelle
moléculaire.
FITGS
LOI„'fitgs'
'Nom du spectre xy0 à fitter' ª xy0„Œ dimx„½x1„xy0[;1]
fgs„x1,[1.5]xy0[;2]÷+/xy0[;2]
©
L1:'Abscisses des maxima (xc) :' ª
d„(nb„½xc„Œ),1
nb,'demi-largeurs gaussiennes (‘x) : ' ª
‘x„Œ
nb,'intensités relatives (ir) : ' ª
ir„ir÷+/ir„Œ
COEF„(1+3×nb)½1
'Nombre max. d''itérations :' ª NITMAX„Œ ª
NIT„0
©
L2:C„fgs[;2] marq COEF ª coef„C
PLOTFIT tabl1„fgs,FGS
'Itérations supplémentaires? : ‘NIT¬0'
–(0¬‘NIT„Œ)/'NITMAX„NIT+‘NIT
ª COEF„coef ª …L2'
xC„xC[ind„“xC]
ª iR„iR÷+/iR„iR[ind] ª ‘X„sigma[ind]
©
'Ecart-type×1E6 : ',STANDEV
1E6×tabl1[;2 3]
'Paramètres initiaux,paramètres optimisés :'
'Position des maxima (xc,xC), demi-largeurs'
'gaussiennes (‘x,‘X),intensités relatives
(ir,iR) :'
©
(xc,[1.5]xC),(d½'*'),(‘x,[1.5]‘X),(d½'*'),ir,[1.5]iR
xyn„*¯0.5×D×D„(x1°.-xC)÷E„(dimx½1)°.בX
1 NORMXYN x1,xyn÷E© normalisation des gaussiennes
PLOT tabl2„fgs,(0 1‡ampl×XYN)×(dimx½1)°.×iR
'Autres valeurs initiales? [1]' ª …(1=Œ)/L1
L'ajustement
d'une somme de gaussiennes au spectre à simuler est effectuée
par la fonction marq,
adaptée d'une fonction utilisant l'algorithme de Marquardt [2] écrite par Mike Jenkins [3]. Cette fonction
fait appel à la fonction fitgs qui
calcule à chaque itération de marq le spectre à comparer au spectre expérimental jusquà
atteindre l'écart-type minimum avec celui-ci.
Z„fitgs C
sigma„‘x×|C[¼nb] ª xC„xc×C[nb+¼nb]
©
© --- calcul des Gaussiennes FGS :
©
FGS„*¯0.5×ARG×ARG„(x1°.-xC)÷(dimx½1)°.×sigma
FGS„FGS÷(dimx½1)°.×sigma
FGS„FGS+.×iR„ir×|C[nb+nb+¼nb]
FGS„Z„(ampl„|C[1+3×nb])×FGS÷+/FGS
©
© --- Evolution de l'écart-type avec le nombre
© d'itérations:
–(0=50|NIT„NIT+1)/'NIT,1E6×STANDEV
fgs[;2],[1.5]FGS'
Le vecteur C dont les éléments sont initialisés à 1
représente les facteurs ajustés par marq
pour optimiser les positions, largeurs et intensités relatives des gaussiennes.
Dans le cas très défavorable d'un spectre non structuré comme celui représenté
sur la figure 3, rien ne permet de connaître les valeurs approximatives de ces
paramètres. On initialise alors le calcul en choisissant un nombre arbitraire
de gaussiennes également espacées, de même largeur et de même intensité et l'on
effectue plusieurs essais pour trouver leur nombre optimum sur le critère des
moindres carrés.
Linterprétation des spectres expérimentaux est
lobjectif final des simulations avec
ajustement automatique des spectres calculés. Des programmes APL réalisés dans
ce but sont décrits dans la réf. [4]. Ils comportent comme FITGS une fonction principale pour linitialisation
des paramètres et la sortie des
résultats qui appelle la fonction marq. Celle-ci
optimise ces paramètres par lintermédiaire dun module de calcul analogue à fitgs. Au lieu de choisir empiriquement
les paramètres initiaux, ces paramètres sont évalués à partir de modèles
théoriques propres à chaque spectroscopie. Laccord entre le spectres expérimental et la spectre calculé est indispensable pour
valider le modèle choisi et les paramètres obtenus.
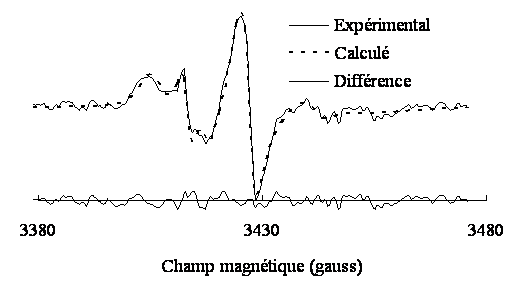
Figure 4. Spectre RPE dun radical nitroxyde dans une membrane
de phospholipide. Le spectre expérimental est celui de la figure 2-III.
Le second exemple
dapplications de programmes APL de simulation est extrait dune étude de résonance
paramagnétique électronique, en collaboration avec le Dr. Wolf du C.H.U. St.
Antoine. Les paramètres obtenus par simulation spectrale (figure 4) donnent des informations sur la polarité ,
lorientation moyenne des molécules par rapport à la surface de la membrane
(ordre moléculaire) et la viscosité au
voisinage dun radical nitroxyde utilisé comme "sonde". En faisant la
même expériences avec plusieurs sondes, on peut évaluer certaines propriétés
physico-chimiques à différentes distances de linterface membrane/eau.
Références
1 - Chachaty C. Les
Nouvelles dAPL, 15 (1995)
18-26.
2 - Marquardt D.W. J.
Soc. Ind. Appl. Math. 11 (1963) 431-441.
3 - Jenkins M.A. APL Implementation
of the Levenberg-Marquardt Algorithm,
C.E.N. de Saclay (1978).
4 - Chachaty C. et Soulié E.J. J. Phys. III France, 5
(1995) 1927-1952.