PROGRAMMES
POUR LES APPLICATIONS PHYSICO-CHIMIQUES DE
CLAUDE CHACHATY
Un ensemble de programmes de simulation a
été écrit en langage APL pour de multiples applications de la résonance
magnétique à la physico-chimie de la matière condensée : phase liquide,
milieux vitreux ou polycristallins et cristaux liquides Ils concernent la
résonance paramagnétique électronique (RPE) (1,2) ainsi que la
résonance et la relaxation magnétique nucléaires (RMN)(1,3,4)
dans les domaines où ces techniques sont complémentaires de
Ces programmes ont pour but daider à lanalyse
des spectres et de déterminer les paramètres spectroscopiques (tenseurs
magnétiques) et dynamiques (temps de corrélation de réorientation) que lon
peut en extraire. Ils sappliquent aux domaines suivants
-Spectres
de radicaux, états triplets et biradicaux, ions paramagnétiques de spin électronique
1/2 (RPE) ou de nimporte quel noyau (RMN) en matrices rigides pour déterminer
les paramètres spectroscopiques.
-Spectres
de radicaux et biradicaux en phase liquide avec calcul des largeurs de raies en
fonction des temps de corrélation de réorientation ainsi que de léchange entre
spins électroniques.
-Temps
de relaxation ![]() et
et ![]() nucléaires en fonction
des temps de corrélation de réorientation et des mouvements intramoléculaires
dans les liquides et les cristaux liquides.
nucléaires en fonction
des temps de corrélation de réorientation et des mouvements intramoléculaires
dans les liquides et les cristaux liquides.
-Spectres
RPE de sondes paramagnétiques nitroxydes
et spectres de RMN de 2H,
Pour la plupart ces programmes présentent deux
options :
-Simple
simulation pour étudier leffet de différents paramètres sur la forme dun
spectre et faire une évaluation préliminaire de leurs valeurs par comparaison
avec le spectre expérimental.
-Optimisation
des paramètres avec ajustement automatisé du spectre simulé au spectre expérimental
en utilisant lalgorithme de Levenberg-Marquardt(5).
Il existe
plusieurs zones non décrites ici comportant des programmes utilitaires :
fonctions graphiques, transformée de Fourier, déconvolution de spectres, échange
de fichiers avec dautres applications Windows etc
Toutes les
zones de travail existent en deux versions : APL2 (IBM) et APL+WIN
(APL2000) et sont disponibles sur demande auprès de lauteur qui assure laide
scientifique et technique en particulier pour modifier un programme en vue
dune nouvelle application. Le logiciel
APL lui-même ne peut être fourni avec les logiciels de RPE et de RMN. On
peut se le procurer auprès dIBM (www.ibm.com/software/ad/apl), dAPL2000 (www.apl2000.com) ou dun fournisseur local.
Le choix dAPL comme langage de
programmation est motivé par les raisons
suivantes :
-Bien adapté à lalgèbre matricielle
(APL = Array Programming Language) très utilisée en résonance magnétique.
-Programmation simplifiée par lexistence
dune variété dopérateurs.
-Fonctionne en mode interactif
permettant une comparaison rapide entre les données expérimentales et les
données calculées avec un accès facile aux paramètres à modifier.
-Messages derreur très explicites
permettant de poursuivre un calcul après correction.
Lutilisation des programmes nécessite
seulement de connaître quelques symboles
APL.
1 Résonance Paramagnétique Electronique.
HRESOL - Spectres à haute résolution de
radicaux en milieu fluide avec couplage hyperfin (CHF) de plusieurs noyaux de
spin quelconque, avec prise en compte du déplacement de second ordre des raies
de résonance et de la dépendance de leur
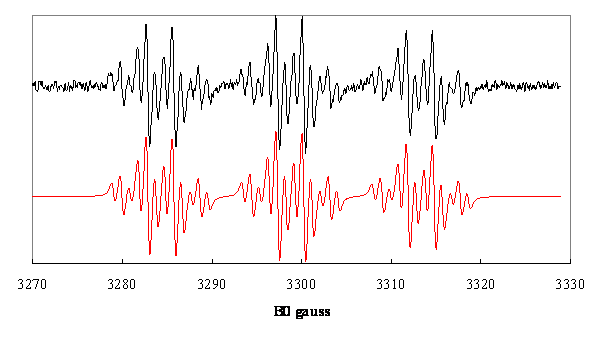
largeur en fonction du nombre quantique magnétique 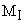 du noyau présentant le plus grand couplage hyperfin.
du noyau présentant le plus grand couplage hyperfin.
Figure 1. Spectres
expérimental et simulé du radical ![]() dans le méthyltétrahydrofuranne
irradié par γ à 77 K puis réchauffé à 295 K .Les valeurs optimisées des constantes de couplage hyperfin sont
dans le méthyltétrahydrofuranne
irradié par γ à 77 K puis réchauffé à 295 K .Les valeurs optimisées des constantes de couplage hyperfin sont ![]() .
.
RIGMAT- Concerne les spectres de radicaux ou ions de spin électronique S = 1/2 en matrice rigide vitreuse ou polycristalline dans les cas suivants:
1
Anisotropie du tenseur spectroscopique
g sans couplage hyperfin.
2
Anisotropie du tenseur g et du ou
des tenseur(s) de couplage hyperfin A
de 1 ou 2 noyaux avec déplacement du second ordre des raies de résonance, les
axes principaux de ces tenseurs étant supposés communs.
Dans ces deux cas les valeurs principales optimisées des tenseurs g et A peuvent être obtenues par simulation automatisée des spectres.
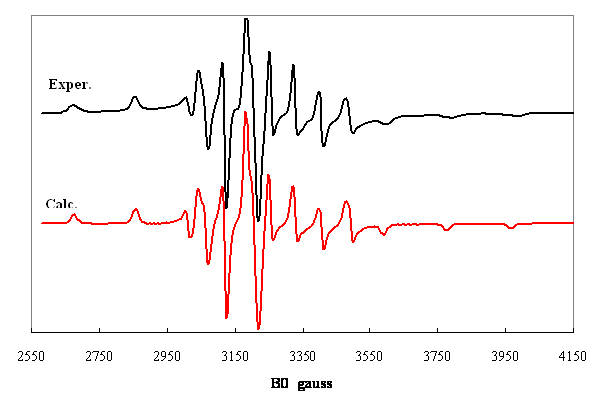
Figure 2. Spectre de lion ![]() dans un gel réticulé de
poly(4-vinyl pyridine) à 250 K.
dans un gel réticulé de
poly(4-vinyl pyridine) à 250 K.
Valeurs principales optimisées des tenseurs A et g :
![]() , .
, .![]() .
.
Laxe Z est dirigé selon la liaison V-O.
3 Orientations quelconques dans un référentiel
moléculaire du tenseur g et des
tenseurs de couplage hyperfin de plusieurs noyaux de spins quelconques. Pour
les noyaux de spin I = 1/2 on prend en
compte les raies satellites résultant des transitions interdites ![]() ,
, ![]() . Les simulations de spectres sont basées sur le traitement
par perturbation du second ordre de lHamiltonien de spin par Iwasaki(6).
. Les simulations de spectres sont basées sur le traitement
par perturbation du second ordre de lHamiltonien de spin par Iwasaki(6).
Figure 3. Spectre du radical allyle ![]() polyorienté
polyorienté
: transitions ![]()
transitions ![]() seulement.
seulement.
Valeurs
principales des tenseurs de couplage hyperfin des protons :
![]() (G)
(G)
![]() 2.5 6.1 4.3
2.5 6.1 4.3
![]() -6.4 -18.9 -12.5
-6.4 -18.9 -12.5
![]() -5.8
-17.8 -13.0
-5.8
-17.8 -13.0
Provenant
de C. Heller et T. Cole, J. Chem. Phys.
33, 243 (1962).
.Pour chaque proton laxe principal Z de ces tenseurs est perpendiculaire au plan du radical, laxe X étant dirigé selon la liaison C-H.
DISTRIB. Correspond aux options 1 et 2 de RIGMAT, mais pour des
systèmes partiellement orientés :
-Distribution Gaussienne des
angles polaire et azimuthal de ![]() .
.
dans le système XYZ des axes principaux des tenseurs a et
g
-Distribution gaussienne dorientations autour dun axe quelconque.
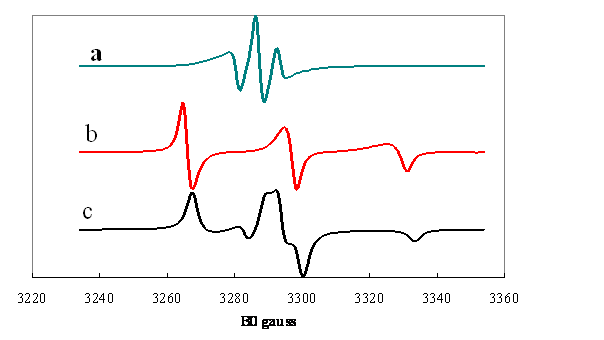
Figure 4. Spectres calculés
pour un radical nitroxyde :
a et b : distribution Gaussiennes des angles
polaire et azimuthal ![]() de
de ![]() dans le référentiel
XYZ centrées sur
dans le référentiel
XYZ centrées sur ![]() (a),
(a), ![]() (b) pour un écart-type
(b) pour un écart-type
![]() .
.
c : distribution sphérique (isotrope) dorientations.
MULTIP- Spectres détats triplets,
biradicaux et paires de radicaux ou dions en matrice rigide pour les
transitions ![]() et
et ![]() . Différents programmes sont utilisables selon la symétrie du
système et lexistence ou non de couplages hyperfins. Dans le cas où le tenseur
g, le tenseur dinteraction
dipolaire, et les tenseurs de couplage hyperfin nont pas les mêmes orientations le spectre est calculé suivant le
traitement par perturbation du second ordre dIwasaki.(6).
. Différents programmes sont utilisables selon la symétrie du
système et lexistence ou non de couplages hyperfins. Dans le cas où le tenseur
g, le tenseur dinteraction
dipolaire, et les tenseurs de couplage hyperfin nont pas les mêmes orientations le spectre est calculé suivant le
traitement par perturbation du second ordre dIwasaki.(6).
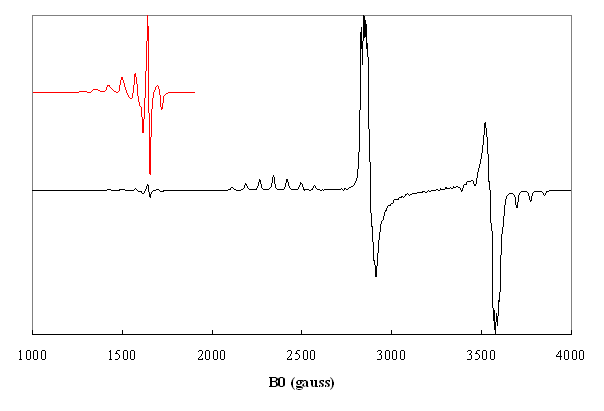
Figure5. Spectre dune paire
dions ![]() dans loxyde CuCe calculé pour les transitions
dans loxyde CuCe calculé pour les transitions ![]() avec les paramètres de
dégénérescence en champ nul D =
avec les paramètres de
dégénérescence en champ nul D = ![]() ,
, ![]() (A.Aboukais,E. Abi-Aad, A. Bennani, C. Chachaty, J-P.
Bonnelle, J. Chem.Soc. Faraday Trans. 91, 3299 (1995))
(A.Aboukais,E. Abi-Aad, A. Bennani, C. Chachaty, J-P.
Bonnelle, J. Chem.Soc. Faraday Trans. 91, 3299 (1995))
BIRAD- Spectre dun biradical
dont les groupes radicalaires sont reliés par une chaîne
alkyle. Linteraction déchange entre les deux spins électroniques varie
rapidement avec leur distance et dépend du recouvrement des orbitales dans
lesquelles ils sont localisés. Cette interaction modulée par
lisomérisation trans¬®gauche autour des liaisons de la
chaîne provoque une alternance des largeurs de raies. La simulation optimisée
des spectres expérimentaux complétée par des mesures des temps de relaxation T1 des
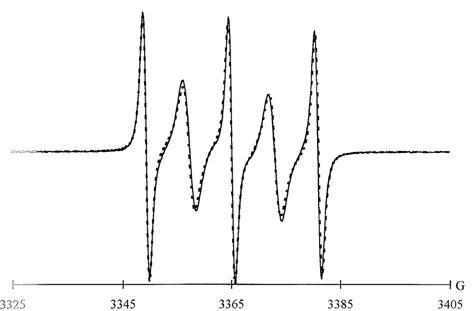
Figure 6. Spectres
expérimental () et calculé (- - - - ) du biradical
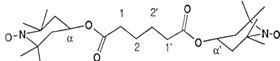
dans le tétrahydrofuranne à 353 K (C. Chachaty, S.
Gambarelli et A. Rassat, Magn. Res. in Chem 33, S174
(1995)).
HMLT- Lorsque le couplage hyperfin dun noyau ou le couplage dipolaire
entre deux spins électroniques dépasse environ 10% de lintensité du champ
magnétique directeur, le calcul de la position des raies de résonance par la
méthode de perturbation du second ordre manque de précision. Les valeurs
précises de la position des raies de résonance sont données par les transitions
entre les niveaux dénergie du système de spins calculés en fonction de
lintensité du champ magnétique par diagonalisation de la matrice de lHamiltonien
de spin. Cette méthode est appliquée ici aux spectres de radicaux libres en
phase liquide et aux états triplets ou aux biradicaux.
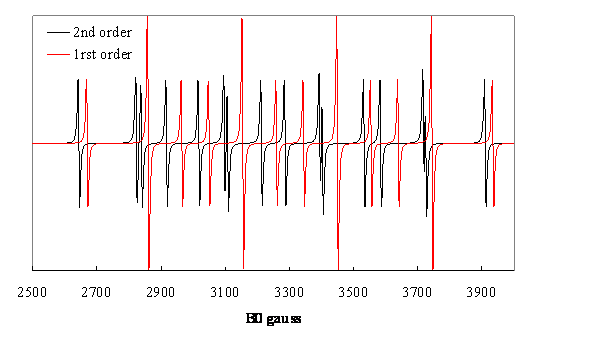
Figure 7. Spectres de 1er et 2ième ordre de ![]() calculés avec
calculés avec ![]() ,
, ![]() , constantes de
couplages provenant de W. Nelson et W. Gordy, J. Chem. Phys. 51, 4710, (1969).
, constantes de
couplages provenant de W. Nelson et W. Gordy, J. Chem. Phys. 51, 4710, (1969).
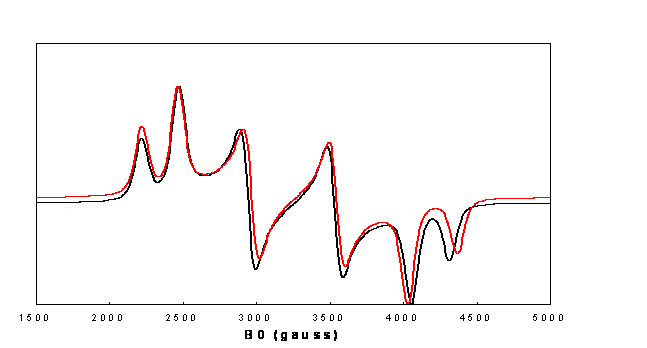
Figure 8.
Spectres de létat triplet du naphtalène polyorienté,
transition
DM=±1 calculés avec
D =
: Diagonalisation de la matrice de lHamiltonien de
spin,
perturbation du second ordre de lHamiltonien de spin(6).
![]() ) en milieux isotropes pour les cas suivants :
) en milieux isotropes pour les cas suivants :
-Réorientation rapide.
-Réorientation lente (diffusion brownienne) selon le
modèle déchange multisites de McConnell et coll.(7).
-Réorientation lente avec distribution de temps de
corrélation, pour les polymères par exemple.
-Echange dune sonde paramagnétique entre un milieu
fluide et un milieu visqueux ou semi-rigide. La simulation optimisée de
spectres expérimentaux donne en particulier les temps de corrélation de
réorientation, la vitesse déchange et la population des sites.
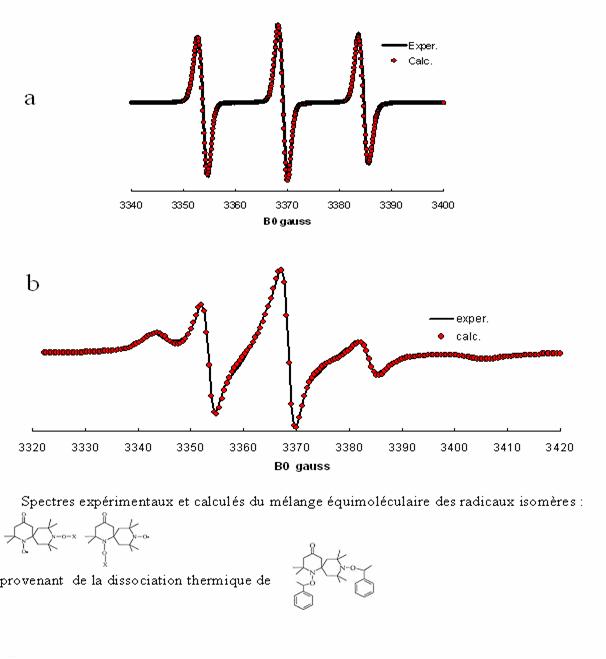
Figure 9. a
Spectre initial des radicaux isomères dans le styrène à 293 K, simulé pour ![]() ,
, ![]() et
et ![]() . X désigne le groupe styryle.
. X désigne le groupe styryle.
b En cours de
polymérisation. Le groupe X est alors la chaîne de polystyrène. La simulation
du spectre indique lexistence de deux fractions de temps de corrélation de
réorientation respectifs ![]() (18%) et
(18%) et ![]() (C. Chachaty, Wenli
Huang, L. Marx, B. Charleux, A. Rassat, Polymer, 44, 397 (2003)).
(C. Chachaty, Wenli
Huang, L. Marx, B. Charleux, A. Rassat, Polymer, 44, 397 (2003)).
FNJP
-Réorientation dun radical par sauts damplitudes
finies.
-Echange dun radical entre 2 ou 3 conformations.
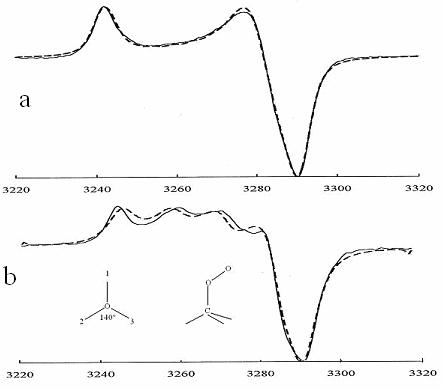
Figure 10. .Spectres
expérimentaux () et calculés (- - - - -) du radical peroxyle dans le
polypropylène.
a Vitesses de saut du
groupe O-O entre 3 orientations ![]()
b
![]() ,
,![]() ,
,
![]() .
.
LQCR- RPE de sonde paramagnétiques dans les phases cristallines liquides anisotropes(1,2) pour les cas suivants:
-Phase
unique nématique, lamellaire ou hexagonale.
-Echange
dune sonde entre une phase anisotrope et une phase isotrope (liquide isotrope
ou phase cubique).
-Echange
entre deux sites anisotropes.
Pour une
réorientation rapide de la sonde, la simulation automatisée des spectres
expérimentaux donne principalement le paramètre dordre moléculaire et les
temps de corrélation de réorientation de la sonde. Dans le cas dun échange, on
obtient également la vitesse déchange et la population des sites. Lorsque la réorientation
est lente on détermine seulement les largeurs de raies et le paramètre dordre moléculaire que lon peut
utiliser comme paramètres initiaux pour déterminer les temps de corrélation en
simulant les spectres avec le programme NLSL de Freed et coll.(8)
accessible depuis cette zone de travail dans la version APL+WIN.
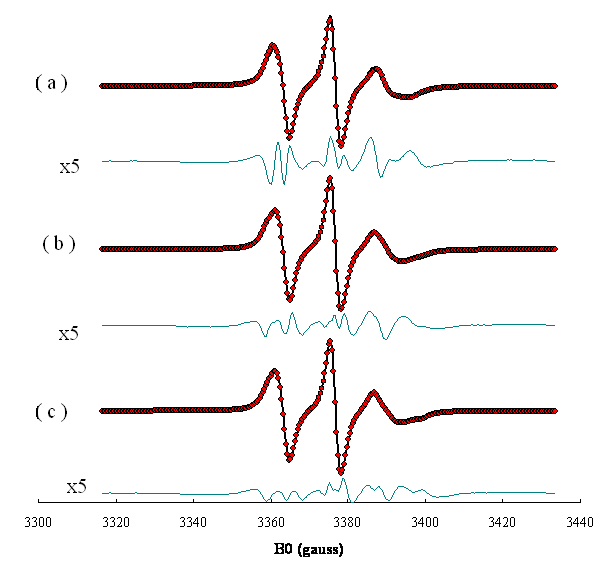
Figure 11-Spectres
expérimentaux (), simulés (◦
◦ ◦ ◦ ◦) et leurs différences amplifiées 5 fois (x5) de
la sonde de phosphatidylcholine marquée par un radical
doxyle en position 14 de la chaîne sn2
(PC14) dans une bicouche de sphingomyéline
contenant 17mol% de cholestérol à ![]() et du temps de correlation de réorientation
et du temps de correlation de réorientation ![]() sont :
sont :
( a ) Dans lhypothèse
dun seul site: ![]() = 0.21,
= 0.21, ![]() =
0.95 ns.
=
0.95 ns.
( b ) Pour 2 sites sans échange : fraction site I :
0.34, site I: ![]() = 0.33,
= 0.33, ![]() = 0.59 ns, site II:
= 0.59 ns, site II: ![]() = 0.14,
= 0.14, ![]() = 1.0 ns
= 1.0 ns
( c ) Pour 2 sites avec échange : fraction site I 0.52, vitesse déchange I↔II ![]() , site I :
, site I : ![]() = 0.36,
= 0.36, ![]() = 0.45 ns, site II:
= 0.45 ns, site II: ![]() = 0.14,
= 0.14, ![]() = 1.2 ns.
= 1.2 ns.
Lécart-type
entre le spectre expérimental et les
spectres simulés sont (a) σ = 1%, (b) σ = 0.65%, (c)
σ = 0. 35%.
DOXYL- Simulation des spectres du
radical doxyle lié en différentes position dune
chaîne flexible, par exemple la chaîne sn2
dun phospholipide dans la phase lamellaire dune membrane
(9).
Les
paramètres ajustables sont le paramètre dordre moléculaire et les temps de
corrélation de réorientation globale de la sonde, les populations du rotamère trans autour des liaisons C-C et les
vitesses des mouvements segmentaires. Tous ces paramètres peuvent être obtenus
par simulation optimisée des spectres prenant en compte les conformères les
plus probables représentant au moins 90% de leur population totale. Les
programmes fonctionnent selon les mêmes principes que ceux de la zone CHAINE décrite plus loin.
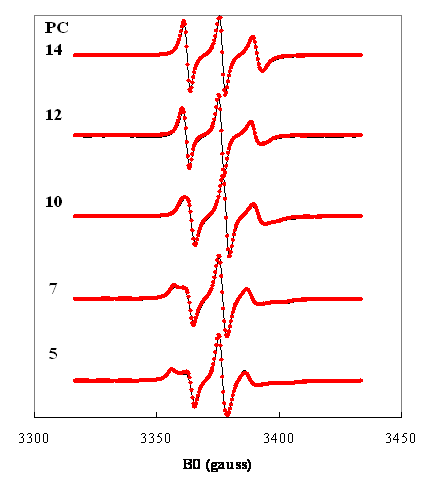
Figure 12. Spectres expérimentaux () et simulés () de la
phosphatidylcholine (PC) marquée par un groupe doxyle en positions 5 à 14 de la chaîne sn2 dans une bicouche de sphingomyéline
à 326 K(9).
2-
Résonance et relaxation nucléaires
RMN1-Spectre RMN dun noyau de spin quelconque en matrice rigide ou dans un cristal liquide. Les largeurs de raies sont ajustées empiriquement ou calculées en fonction des temps de corrélation de réorientation moléculaire(1).
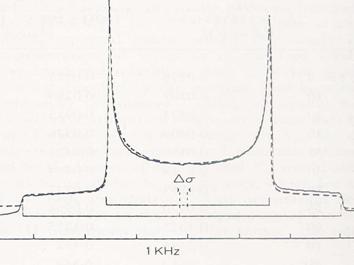
Figure
13. Spectres expérimental () et simulé (- - - - -) de ![]() de leau dans un
cristal liquide de dibutylphosphate/
de leau dans un
cristal liquide de dibutylphosphate/![]() à 230 K. Paramètre dordre moléculaire : 0.049,
anisotropie de déplacement chimique de
à 230 K. Paramètre dordre moléculaire : 0.049,
anisotropie de déplacement chimique de ![]() :
: ![]() -1.37
ppm (C. Chachaty, J.P. Quaegebeur, Mol. Phys. 52, 1081 (1984)).
-1.37
ppm (C. Chachaty, J.P. Quaegebeur, Mol. Phys. 52, 1081 (1984)).
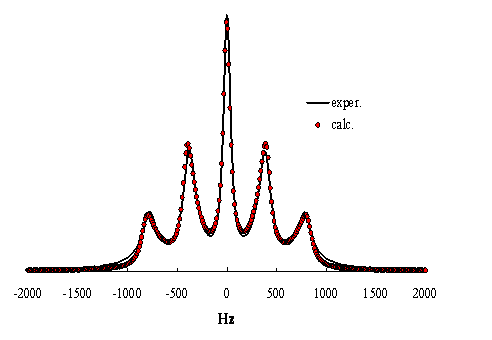
Figure
14. Spectre de loxygène 17 de ![]() adsorbé sur le DNA à 333
K . Le spectre expérimental provient de A. Catte,
Université de Cagliari, Italie. Les paramètres optimisés par simulation de ce
spectre sont
adsorbé sur le DNA à 333
K . Le spectre expérimental provient de A. Catte,
Université de Cagliari, Italie. Les paramètres optimisés par simulation de ce
spectre sont ![]() pour laxe de symétrie
moléculaire dont le temps de corrélation de réorientation est
pour laxe de symétrie
moléculaire dont le temps de corrélation de réorientation est ![]()
RMN2- Spectre RMN dun noyau de spin 1/2 ou 1 pour une réorientation
moléculaire lente en milieu isotrope. On utilise le modèle de diffusion
brownienne ou de sauts aléatoires damplitudes
finies comme pour les programmes des zones BRNDF et FNJP.
RELAX- Calcul des temps de
relaxation T1 et T2 dun noyau de spin 1/2 ou 1 dans une molécule rigide en
réorientation dans un liquide ou dans un segment de macromolécule flexible.
Dans ce dernier cas, on peut choisir différentes fonctions de
distribution des temps de corrélation de réorientation.
CHAINE- Relaxation dipolaire ou
quadrupolaire des carbones 13 , des protons ou des
deutérons dune chaîne alkyle liée à une tête polaire (par ex. groupes ![]() ,
, ![]() ou
ou ![]() ) en réorientation dans un liquide ou dans un cristal liquide(4,10).
) en réorientation dans un liquide ou dans un cristal liquide(4,10).
-Ecarts dipolaires ou quadrupolaires des raies de ces mêmes noyaux dans un cristal liquide(10).
-Relaxation dipolaire ou déplacement de
pseudocontact des carbones 13 ou des protons de la chaîne induits par un ion
paramagnétique fixé à la tête polaire(3, 11).
-Relaxation dipolaire dun noyau de spin 1/2 de la
tête polaire (par ex. phosphore ou azote 15) par les protons de la chaîne
alkyle.
Les calculs de ces observables sont basés sur le modèle de lisomérisation trans¬®gauche autour de chaque liaison C-C de la chaîne.
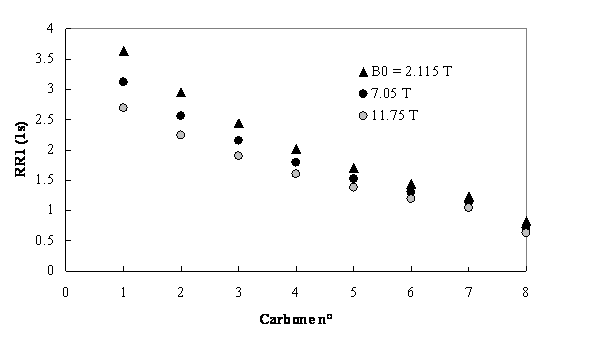
Figure 15. Vitesses de relaxation longitudinale des
carbones 13 de la chaîne alkyle de loctylphosphate de pyridinium en phase
lamellaire à 300 K. Ces vitesses sont calculées daprès les données de la réf.
(10) avec un paramètre dordre ![]() et des temps de
corrélation de réorientation moléculaire
et des temps de
corrélation de réorientation moléculaire![]() . La population du rotamère trans autour des liaisons
C-C est 0.9 et la probabilité par unité de temps de la transition gauche→trans est
. La population du rotamère trans autour des liaisons
C-C est 0.9 et la probabilité par unité de temps de la transition gauche→trans est
![]() .
.
3-Exécution dun programme.
-Charger
la zone de travail correspondant au problème à traiter
-Entrer
en minuscules le nom de la zone pour avoir la liste des programmes avec leurs
caractéristiques. Ceux-ci existent généralement sous deux formes : simple
simulation pour étudier linfluence des paramètres spectroscopiques et/ou
dynamiques sur la forme des spectres ou détermination des valeurs optimisées de
ces paramètres par simulation automatisée dun spectre expérimental.
-Entrer le nom du programme choisi. Celui-ci
appelle généralement un sous-programme pour introduire ou modifier les
paramètres, autrement cela est effectué par étapes au cours de lexécution du
programme principal.
Exemple :
(les commentaires non inclus dans le programme sont inscrits
en rouge entre crochets.)
)LOAD RIGMAT [Charger la zone (workspace)]
SAVED 2005-12-23 13.58.02
(GMT-5)
NONAX1F [Afficher le nom du programme choisi puis ↓ Entrée]
Is
the spectrum a DOS file ? [1]
:
0
Name of the spectrum :
:
RTM125 [le
tableau XY correspondant existe déjà dans la zone]
Number
of points : 528
Baseline
correction ? [1]
:
0 [ligne
de base déjà rectifiée]
Normalized
spectrum : XY, integral : IXY
Second
moment (M2) :
60048.8
Hm for g = g0 : 3248 [Hm donne approx.le centroïde du spectre]
Spectral range about Hm :
-669 912
NONAX1F_IN [cliquer sur ce nom pour éditer les paramètres initiaux et les modifier éventuellement]

[Terminer
lédition/correction des données par ↓ clé
F4 puis ↓ Entrée.Les données initiales sont
récapitulées ci-dessous]
gZZ, gYY, gXX : 1.9375 1.973 1.974
g0 : 1.9615
Field
H0 g = 2.00232 :
3181.78
Frequency : 8.91681 GHz
Correction to H0? : DH0≠0 : 35
Field
Hc for g0 = 1.9615 :
3248
Total
nuclear spin :
3.5
Relative
line intensities :
1 1 1 1 1 1 1 1
aZZ,aYY,aXX (a,gauss) : 185 71 66
a0 = 107.333
Second
order ? [1] : 1
Angular
range of θ: 0 90
Uneven
number of orientations
91
Standard dev. of Gaussian distrib. of θ (dth≠0) : 0
Lorentzian
[1] or Gaussian [2] lineshape ? 1
Linewidths ∆HRzz, ∆HRyy,
∆Hxx : 5 5 5
Stand.
dev. of the Gaussian broadening
or half width of the Lorentz. broadening
(∆HGL) : 3
Integral ? [1] : 0
Automated fit?[1] [si 0 simulation préalable du spectre pour bien centrer le
spectre calculé/spectre expérimental et vérifier la validité des données
initiales]
:
1
Iteration max. number :
:
120
[Ecart-type
normalisé entre spectre exper. et spectre calc., vs
nombre ditérations]
10 13.6243
20
12.6999
30
9.84888
40
3.92905
50
3.94236
60
2.44939
70
2.30148
80
2.27829
90
2.28054
100
2.26737
110
2.26128
120
2.25777
130 2.25776

More iterations ? :
:
0 [si
loptimisation ne progresse plus ignificativement]
Name
of the XY1..N table
SP1 [donner un nom aux
spectres exp. et calc. pour les conserver dans 1a zone ou les tracer
ultérieurement sur Excel]
Iteration
number : 131
Calc.
time (s) :
399.593
Input
parameters [1], manual↔automated fit [2]
Optimized
parameters [3], replot [4], Excel [5]
:
3
Title?
RTM125
NONAX1F
* RTM125 * 23
12 2005
Standard
deviation![]() 100 : 2.2556
100 : 2.2556
H0
(g = 2.0023) :
3216.8
gzz, gyy, gxx and g0 : 1.9377 1.9732
1.9742 1.9617
Nuclear
spin : 3.5
azz, ayy, axx and a0 : 184.19 68.856
64.368 105.8
Spectral
window and resolution : 2579 4160 3
∆HRzz, ∆HRyy, ∆Hxx Lorentz. : 6.9886 3.2892 7.936
Gaussian broadening : 3.7668
[convolution du spectre calculé par une Gaussienne]
Input
parameters [1], manual↔automated fit [2]
Optimized
parameters [3], replot [4], Excel [5]
:
0
---------------------------------------------------------------Another
spectrum ? [1]
:
0
4 Références
4. J.Ph Caniparoli, A.
Grassi, C. Chachaty.. Mol.. Phys. 63, 419 (1988).
b. D.W. Marquardt, J.
Soc. Ind. Appl. Math. 11,
431 (1963).
6
M. Iwasaki, J. Mag. Res. 16, 417
(1974).
7. R.C. McCalley,
E.J. Shimshick, H.M. McConnell, Chem. Phys. Letters, 13, 115 (1972).
8. D.E. Budil, S. Lee, S. Saxena, J.H.
Freed. J. Magn. Res. Series A. 120,: 155 (1996).