Tirages
aléatoires uniformes et gaussien
par Charles Hubert
Généralités
On décrit ici
des fonctions qui effectuent des tirages aléatoires uniformes dans un
intervalle, sur un cercle, dans un disque (limité par un cercle), sur une
sphère et dans une boule (limitée par une sphère), et des tirages gaussiens.
Conventionnellement les majuscules désignent des variables aléatoires, les
minuscules désignent des variables ordinaires.
Pour une
variable aléatoire X prenant ses valeurs dans un intervalle [a,b], pouvant être infini, on définit sa fonction de
répartition f(x) par la probabilité que X soit inférieure ou égale à x :
![]()
Si cette
fonction f(x) est dérivable, sa dérivée f'(x) est la densité de probabilité de
X ; alors f'(x)dx est la probabilité que X soit
dans l'élément de longueur dx centré sur x.
La fonction
de répartition est croissante ; si on fait le changement de variables
![]()
on voit que
![]()
ce qui montre que U est distribuée uniformément dans
l'intervalle [0,1] ; sa densité de probabilité est 1.
Si on sait
programmer la réciproque ![]() de f, on en déduit un moyen de générer des
tirages de fonction de répartition f : on tire des valeurs U
uniformément réparties dans [0,1] et on calcule les valeurs
de f, on en déduit un moyen de générer des
tirages de fonction de répartition f : on tire des valeurs U
uniformément réparties dans [0,1] et on calcule les valeurs
![]()
Voyons des
applications.
Tirage
uniforme dans un intervalle
On sait que
la primitive APL "?" tire des valeurs uniformément réparties dans
l'ensemble des n premiers entiers naturels. En prenant n très grand et en
divisant par n les valeurs tirées on ramène ces valeurs à
l'intervalle [0,1]. En multipliant par a‑b et en retranchant de a on
ramène ces valeurs à [a,b].
La fonction
qui fait ce tirage est
![]()
le résultat "X" a pour dimension
"dim" et est tiré dans [a,b] ou [b,a] ; b vaut 0 par
défaut.
Tirage
uniforme sur un cercle
Sur un cercle
de rayon r et de centre (x,y), on tire des
valeurs Θ uniformément réparties dans [‑π,+π] et on
calcule
![]()
La fonction
qui fait ce tirage est
![]()
le résultat "X" a pour dimension
"dim,2" ; x et y valent 0 par défaut.
Tirage
uniforme dans un disque
Dans un
disque de rayon 1 et de centre (0,0) la densité de probabilité est
1/π. En coordonnées polaires, l'élément d'aire étant
r dr dθ, la probabilité de cet élément d'aire s'écrit
![]()
C'est le produit d'une différentielle en r par une différentielle en θ et
les bornes des deux variables sont indépendantes ; les variables R et
Θ sont donc indépendantes. Θ est
uniformément répartie dans [‑π,+π]. La
fonction de répartition de R est
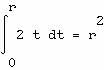
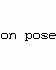
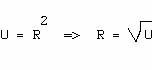
On tire donc
des valeurs uniformément réparties U dans [0,1], Θ dans [‑π,+π] et pour un disque de rayon a et de centre (x,y) on
calcule
![]()
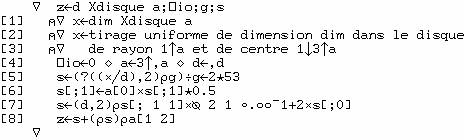
La fonction
qui fait ce tirage est
![]()
le résultat "X" a pour dimension
"dim,2" ; x et y valent 0 par défaut.
Tirage
uniforme sur une sphère
Sur une
sphère de rayon 1 et de centre (0,0,0) la densité
de probabilité est 1/4π. En coordonnées polaires, l'élément d'aire étant
cos θ dθ dφ, la probabilité de cet élément d'aire
s'écrit
![]()
C'est le produit d'une différentielle en θ par une différentielle en
φ et les bornes des deux variables sont indépendantes ; les variables
Θ et Φ sont donc indépendantes.
Φ est uniformément répartie dans [‑π,+π].
La fonction de répartition de Θ est
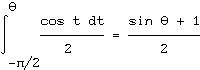
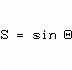
(S+1)/2 est donc uniformément répartie dans [0,1] et S dans [‑1,+1]. Les coordonnées cartésiennes étant
![]()
il n'est pas nécessaire de calculer Θ. Pour
une sphère de rayon r et de centre (x,y,z) on tire
Φ uniformément répartie dans [‑π,+π] et S dans [‑1,+1],
puis on calcule
![]()
![]()
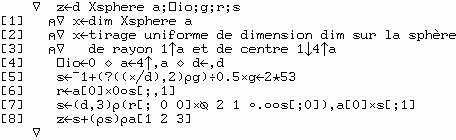
La fonction
qui fait ce tirage est
![]()
le résultat "X" a pour dimension
"dim,3" ; x, y et z valent 0 par défaut.
Tirage
uniforme dans une boule
Dans une
boule de rayon 1 et de centre (0,0,0) la densité
de probabilité est 3/4π. En coordonnées polaires, l'élément de volume
étant ![]() la probabilité de cet élément de volume
s'écrit
la probabilité de cet élément de volume
s'écrit
![]()
C'est le produit de trois différentielles en r, en θ et en φ et les
bornes des trois variables sont indépendantes ; les variables R, Θ et
Φ sont donc indépendantes. Φ est uniformément répartie dans [‑π,+π] et S dans [‑1,+1]. La fonction de
répartition de Θ est
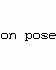
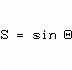
La fonction de répartition de R est
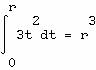
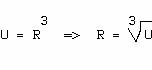
On tire donc
des valeurs uniformément réparties, S dans [‑1,+1],
Φ dans [‑π,+π], U dans [0,1]. Pour une sphère de rayon a
et de centre (x,y,z) on calcule
![]()
![]()
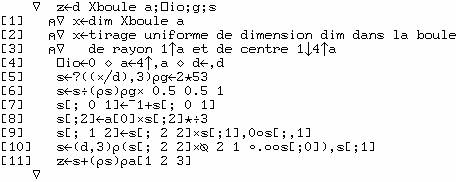
La fonction
qui fait ce tirage est
![]()
le résultat "X" a pour dimension
"dim,3" ; x, y et z valent 0 par défaut.
Tirage
gaussien
La fonction
de répartition d'une variable gaussienne normalisée X, c'est-à-dire de
moyenne 0 et d'écart-type 1, est
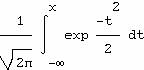
ce n'est pas une combinaison de fonctions
mathématiques élémentaires ; son inversion n'est pas facile.
On évite
cette difficulté en considérant deux variables gaussiennes normalisées X et Y
indépendantes. La densité de probabilité de (X,Y) est
donc
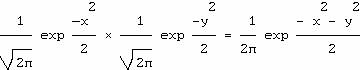
On passe
alors en coordonnées polaires où l'élément d'aire est
r dr dθ ; la probabilité de cet élément d'aire est alors
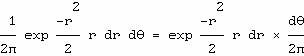
C'est le produit de deux différentielles en r et en θ et les bornes des
deux variables sont indépendantes ; les variables R et Θ sont donc indépendantes. Θ est uniformément répartie dans [‑π,+π]. La fonction de répartition de R est
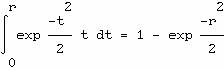
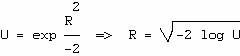
et 1‑U est uniformément répartie dans [0,1[,
donc U l'est dans ]0,1] ; il faut que U ne puisse jamais être nul.
Pour une
variable gaussienne de moyenne m et d'écart-type σ on tire Θ
uniformément répartie dans [‑π,+π] et
U dans ]0,1]. Puis on calcule
![]()
et on fusionne X et Y en un seul tableau.
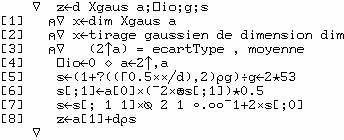
La fonction
qui fait ce tirage est
![]()
le résultat "X" a pour dimension
"dim", pour écart-type sig et pour moyenne m ; m vaut 0 par
défaut.
Les
fonctions