Trucs et Astuces
de
Gérard Langlet
Un moyen simple et pédagogique - sans utiliser la primitive diadique (!) donnant directement, trop facilement dirons-nous, les combinaisons - dimprimer les coefficients du binôme, consiste à utiliser le polynôme x+1 (dont les coefficients sont 1 1 sous forme de vecteur) et à itérer lélévation du polynôme en puissances successives, ce qui donne, en programmation structurée, grâce à la fonction générale MP de multiplication de polynômes[1], écrite en une ligne sans parenthèses :
’ R„A MP B;D;K;V
[1]
A„,A ª D„²K,0—¯1+K„½B„,B ª R„A°.×B ª
V„1-+\K½1 ª R„+/V´R®D½0
’
1 ª
+W„V„1 1 ª '+W„W MP V'do 9
1
1 1
1 2
1
1 3
3 1
1 4
6 4 1
1 5
10 10 5 1
1 6
15 20 15 6 1
1 7
21 35 35 21 7 1
1 8
28 56 70 56 28 8 1
1 9
36 84 126 126 84 36 9 1
1
10 45 120 210 252 210 120 45 10 1
Bien sûr, en imprimant les mêmes résultats modulo 2, ou en remplaçant la fonction MP par MPB (multiplication de polynômes binaires, dans laquelle lopération multiplication devient une conjonction logique et laddition une différence logique donc un Ou Exclusif), on retrouve le triangle - fractal - de Sierpinski :
’ R„A MPB B;b;D;V
[1]A„,A ª
D„²b,¯1+b„½B„,B ª R„A°.^,B ª V„1-+\b½1ª
R„¬/V´R®D½0 1 ª
1+V„W„1 1 ª '+2|W„W MP V'do9 ou
bien:
ª
1+V„W„1 1 ª '+W„W MPB V'do 9
1
1 1
1 0
1
1 1
1 1
1 0
0 0 1
1 1
0 0 1 1
1 0
1 0 1 0 1
1 1
1 1 1 1 1 1
1 0
0 0 0 0 0 0 1
1 1
0 0 0 0 0 0 1 1
1 0 1 0 0 0 0 0 1 0
1
3. POLYNOMES:
Sous APL_SE, APL*PLUS II et III, il est possible de cliquer deux fois sur un nom inexistant dans la session et déditer par défaut cet objet qui devient initialement un vecteur de caractères. Même si, sous léditeur, on crée par exemple un objet de 2 lignes, lobjet en question ne changera pas de type (en labsence de la frappe dune commande de type <Ctrl> A).
Soit donc un objet P vecteur (avec un retour du chariot comme séparateur de ligne) qui simprime sur 2 lignes comme :
P
3
x -1
Un non APListe reconnaîtra sans grande difficulté un polynôme dans le contenu de P.
La fonction POL va convertir un polynôme à une variable, écrit de manière conventionnelle, en vecteur de coefficients par puissances décroissantes de ladite variable (x) de sorte que lon puisse effectuer aisément des traitements en APL :
Bien entendu, P pourrait contenir des espaces ou des parenthèses, et des monômes en nimporte
quel ordre.
POL P
1 0 0
¯1
Bien entendu, il existe dans la zone une fonction inverse LOP qui restitue P sous forme de caractères, exprimé en puissances décroissantes, à partir dun vecteur de coefficients numériques :
LOP 1 0
0
¯1
3
x -1
LOP 6 21 ¯14 0 ¯3 21 ¯8 ¯1 ¯1
8 7 6 4 3 2
6x +21x -14x -3x +21x -8x -x-1
Si la variable Q contient par exemple (les exposants ne sont pas obligatoires) :
x-1
on obtiendra un résultat sous forme polynomiale en écrivant :
P DIP Q
2
x +x+1
ce qui montre au passage que la limite du quotient polynomial, pour x tendant vers 1, vaut 3.
La fonction DIP fait le même travail que la fonction DP,
mais, en plus, rend son résultat sous forme de polynôme en utilisant LOP[2] pour
largument de sortie R.
’ R„A DP B;a;J
[1]
R„0½A„POL A ª J„+/^\0=A ª
a„½A„J‡A ª J„+/^\0=B„POL B ª B„J‡B
[2]
'J„1†AªR„R,J„J÷1†Bªa„½A„1‡A-a†B×J'do
1+a-½B ª 'malªA'do 0Ÿ.¬A
’
(La fonction LOP est
beaucoup plus compliquée - surtout si on essaie de la programmer
vectoriellement - que DP ou
MP - voir le Courrier des Lecteurs pour le listage de cette dernière -
car la notation mathématique conventionnelle, que lon apprend à lécole
regorge dexceptions et dellipses; cest pourquoi K. Iverson imagina... APL.)
La fonction mal émet un son aigu si le reste de la division
polynomiale nest pas identiquement nul. (Le reste se trouve également affiché
dans ce cas).
’ mal
[1]
ŒSOUND 2000 500
’
On nen est pas encore au véritable calcul formel[3], capable de développer des identités remarquables, mais cest un début...
4. On peut faire bien des
choses avec APL_SE!
La Zone COCSE.AWS
Cette petite zone de travail (une vingtaine de K) est en fait un puissant simulateur dAPL étendu à diverses fonctionnalisés utiles pour des démonstrations, en général, et en algèbre binaire en particulier.
Elle contient les fonctions indispensables (tirées de la zone plus importante COCRAY utilisable en APLPLUS, qui en contient plus de 600 mais ne peut se charger sous APL_SE gratuit et plus limité en place-mémoire).
On passe en « session spéciale » grâce à lappel de la fonction INTERP (fonction niladique) dont on peut sortir par la flèche droite (« … »).
En session sous linterprète INTERP , la ligne dexécution vire au rouge
Règles
1°) Une fois le simulateur activé, toute séquence dinstructions présente sur la même ligne dexécution - à condition que les expressions soient séparées les unes des autres par 5 espaces - est considérée, sans aucun séparateur (tel que le diamant), comme séxécutant en parallèle. Bien entendu, sur une machine séquentielle, les exécutions ont lieu lune après lautre et la modification dun résultat dans lune des expressions peut entraîner des résultats imprévus; en général, ce nest pas ce que lon cherche à faire dans une démonstration. Les résultats des expressions peuvent être de taille différente et de type différent. Mais le résultat qui va safficher sera en fait un Vecteur de Résultats, limité pour laffichage à la largeur de lécran soit 80 caractères (voir ci-dessous le point 2°).
2°) Tout objet APL (numérique puisque nous sommes en fait sous APLPLUS) ne contenant que des 0 ou des 1, donc interprétable en binaire, saffiche en pixels, les 1 étant remplacés par des petits pavés (jaunes sur lécran, noirs sur une imprimante) et les 0 étant remplacés par un fond continu (violet sur lécran, blanc sur limprimante).
3°) Lorsque le résultat est un vecteur dobjets, ce résultat prend, en nombre de lignes, la taille du plus grand. On ne peut pas afficher dobjets de plus de 24 lignes (limitation pour les démonstrations). Les objets sont séparés par une barre verticale semi-graphique, laquelle apparaît sur lécran plutôt comme une double barre verticale, négatif de la précédente, à cause du choix des couleurs. Il napparaît quun seul vecteur de résultats même si plusieurs expressions différentes en sont à lorigine; ainsi, lorsquune première expression a pour résultat une hypermatrice, ce dernier résultat peut devenir un vecteur dobjets matrices en nombre égal au nombre de plans de lhypermatrice, et si une seconde expression est exécutée à droite de la même ligne, ses résultats - scalaire ou vecteur dobjets - viendront se concaténer à droite du vecteur dobjets du résultats final.
4°) Sous cet interprète spécial, certains caractères symboliques nont pas la signification usuelle de lAPL.
Le double astérisque
Ainsi, le double astérisque diadique ** de M**N va prendre la signification « élévation de la matrice M, supposée binaire et carrée, à la puissance N en algèbre entière modulo 2 ».
De la même façon, **M (forme monadique) est la puissance du groupe cyclique de la matrice M si celle-ci est binaire[4], carrée et inversible modulo 2. Si la matrice nest pas inversible, la réponse est 0. (Le signe de **M est toujours le déterminant, calculé modulo 2, dune matrice carrée binaire). Lorsque M est inversible, le résultat de M** **M est toujours, par définition, une matrice-unité.
Le double point horizontal
Le symbole « .. » (double point horizontal) considéré comme un symbole unique, correspond, dans son acception monadique, à linversion modulo 2 généralisée de matrice carrée binaire, et dans son acception diadique, au produit matriciel modulo 2 de matrices binaires conformes. : une expression telle que ..M va donc délivrer un résultat que lon obtiendrait - si M est inversible - aussi par 1=|ŽM à condition que M ne dépasse pas un certain rang[5]. Lexpression M.. ..M produit une matrice-unité si M est une matrice inversible. Mais ..M produit toujours un résultat, que M soit inversible ou non ! Il sagit, dans le cas dune matrice non inversible, dune inverse généralisée.
Dans une matrice non inversible, le déterminant est nul; les lignes (ou les colonnes) ne constituent pas une base vectorielle de N vecteurs (si N est le rang), mais il existe en général - sauf pour une matrice identiquement nulle - une sous-base de n vecteurs indépendants, avec n<N. Linverse généralisée obtenue ici - cest une question de choix - est celle qui a ses n vecteurs vraiment indépendants dans les premières colonnes, les colonnes finales étant complétées par les colonnes finales dune matrice-unité de sorte que lensemble des N vecteurs forme à nouveau une base : en conséquence, toute inverse généralisée de matrice non inversible est inversible. En inversant à nouveau cette dernière matrice, on va reconnaître les premières colonnes dune matrice initiale non inversible (parfois décalées à gauche si ladite matrice initiale possédait des colonnes nulles ou bien des colonnes identiques à des colonnes précédentes). Linverse généralisée dune matrice identiquement nulle est alors une matrice-unité de même rang.
On pourra vérifier les identités suivantes (le symbole non APL ÜÞva, dans ce texte, signaler les identités ) :
M**¯1+k×**M ÜÞ ..M si
M est
inversible
M**1+k×**M ÜÞ M si M est inversible
k étant un entier quelconque (négatif, nul ou positif) bien sûr représentable en machine[6].
Ce nest pas difficile : il suffit de juxtaposer, sous linterprète INTERP, les expressions à comparer, séparées par 5 espaces, et de vérifier de visu[7] si lon obtient bien le même résultat.
Autres
fonctions utiles
La conjonction ET
Même hors session INTERP, on peut se servir de la conjonction ET (ici non booléenne) pour former, à partir de A et de B, deux objets quelconques dAPL-ISO, une structure correspondant à un vecteurs dobjets dont les composantes seront A et B. Dailleurs, lexpression monadique ET A forme un vecteur dobjet à une seule composante, laquelle est A. Par extension (et contrairement à ce que feraient les APL étendus), lexpression A ET B ET C engendre un vecteur de trois composantes A, B et C et non pas une structure à plusieurs niveaux, ce qui est beaucoup plus simple... Et ainsi de suite[8]. Dailleurs le véritable fonction de la conjonction ET dans la langue française consiste à créer des vecteurs de concepts et non pas des structures hiérarchiques; si on veut parler de linguistique[9], alors respectons-la.
Initialement, lintérêt était surtout la compression dinformation, parce quAPLPLUS code les booléens en 2 octets, ce qui représente un gâchis formidable bien que relativement efficace en performances.
Supposons que A, B et C soient des matrices carrées binaires, respectivement de rang 16, 15 et 16. On aura 256+225+256 bits soit en tout 737 bits, codés sur 1474 octets dans la zone (du moins pour les seuls contenus des variables). Si on écrit simplement R„A ET B ET C , la dimension de R atteindra seulement 134 octets - soit un gain dun facteur 11. Et plus les objets sont gros, plus le gain est grand; cela vaut la peine dengranger dans 200 k ce que lon devrait mettre dans plus de 2 Mégaoctets de manière conventionnelle.
La zone COCSE contient un tel objet (une variable) dénommée ROBEE. Lorsquon est sous INTERP, lexpression ½ROBEE répond 3, car ROBEE possède bien 3 composantes, lesquelles sont les célèbres ROBY, MAYA et GROBY, artistes bien connus dans ces chroniques, en fait comme par hasard des matrices binaires carrées de rang respectivement 16, 15 et 16.
Dans la même zone COCSE, la variable MAYA existe aussi sous forme de matrice de bits APL-ISO; par contre, les objets ROBY et GROBY ne sont pas des variables mais des fonctions niladiques avec argument de sortie, dont le résultat est la matrice respectivement souhaitée, mais extraite de ROBEE:
|
’ R„ROBY [1] R„dans ROBEE ’ |
’ R„GROBY [1] R„dans FIN ROBEE ’ |
La sous-fonction dans (en anglais « in ») a une syntaxe diadique telle que lexpression 1 dans ROBEE fournit la première composante de ROBEE. Mais le 1 est facultatif en syntaxe monadique, doù son omission. La fonction FIN (version monadique) considère lobjet à partir de sa dernière composante, donc le retourne de lintérieur. GROBY est bien la troisième et dernière composante de ROBEE.
Lintérêt du simulateur INTERP apparaît rapidement lorsquon souhaite faire des démonstrations sous APL*PLUS ou APL_SE car on pourra écrire directement :
ROBEE
et voir les trois matrices dun seul coup dil en pixels, puis reprendre la même instruction (grâce à la gestion décran) et rajouter à gauche .. de manière à voir les trois matrices inverses, puis recommencer en rajoutant encore à gauche .. de manière à inverser les trois matrices une seconde fois. Sachant que MAYA et GROBY sont inversibles mais non pas ROBY, on va reproduire la moitié gauche de ce dernier personnage, tandis que les matrices MAYA et GROBY seront restaurées intégralement.
La fonction HASB
· Linstruction HASB N met dans la variable B un vecteur binaire de dimension N bits. Ceci permet dexpérimenter les fonctionnalités vectorielles décrites dans cette zone.
La fonction HASMI
· Linstruction HASMI N met dans la variable M une matrice binaire de rang N tirée au hasard et garantie inversible. Ceci permet dexpérimenter les fonctionnalités matricielles décrites dans cette zone.
Ces deux instructions nont pas de résultat
Lorsquune instruction est une affectation de variable, le contenu de
cette variable va, au contraire, safficher sous linterprète INTERP.
De même, sous linterprète INTERP, le résultat de lexpression précédemment exécutée se trouve dans une pseudo-variable, toujours accessible dans linstruction suivante grâce au symbole « zilde » Ð, accessible au clavier APL par la combinaison de touches <Alt> $ . (Cette décision un peu arbitraire mais bien pratique provient du fait quon na pas besoin de vecteur numérique vide dans les démonstrations...).
Module FORTRAN
Le calcul de la puissance du groupe cyclique dune matrice binaire inversible fait appel à un module compilé écrit en FORTRAN Microsoft 8 bits (se rappeler quAPL*PLUS est une simple application DOS). Lorsquune matrice M, argument droit de ** est donnée, un fichier appelé MATR.TXT, tout à fait éditable, sert dentrée au module FORTRAN[10]. Le module sappelle par une simple commande programmable CMD'RACRF51' car, bien sûr, il nexiste pas de NA en APL_SE. Le résultat est mis dans le fichier MATR.RES lequel est analysé dans la session pour produire la réponse. Comme ce FORTRAN ne peut coder des entiers super-longs (et quil importe de définir des dimensions maximales), le logiciel ne peut traiter de matrices au-delà du rang 32, ce qui est largement suffisant pour des démonstrations. La puissance P du groupe cyclique dune matrice binaire inversible de rang N ne peut pas dépasser 2N. Pour N égal à 16, P vaut 65535 et sera trouvé en un temps raisonnable : le module FORTRAN est au moins 20 fois plus rapide, lorsque P est suffisamment élevé, que son équivalent APL - à cause des boucles que lon na pas pu éviter jusqualors[11].
Attention : pour une matrice non inversible, le logiciel FORTRAN ne calcule pas dabord le déterminant modulo 2 (évidemment nul); ce nest quaprès dépassement de la limite éventuelle de P imposée par le rang N que le résultat est remis à 0; cest pourquoi le calcul de **ROBY dont le résultat est nul sera plus lent que celui de **GROBY dont le résultat nest pas nul. Mais on peut néanmoins opérer vectoriellement sur ROBEE, vecteur de 3 matrices binaires dont deux sont inversibles modulo 2; le résultat de **ROBEE sera alors un vecteur de 3 entiers, en loccurrence 0 12282 6132 obtenu en une trentaine de secondes sur un IBM Thinkpad 340CSE, (donc un simple 486 portable - sans coprocesseur - à 25 MHz).
Sous INTERP, on pourra expérimenter linstruction : ROBEE** **ROBEE dont le résultat est un vecteur de trois matrices-unité, respectivement de rang 16, 15 et 16. (Le simulateur est même capable de comprendre une instruction telle que (**ROBEE)**ROBEE donc avec des arguments commutés[12].
Toutes les modifications potentielles de la syntaxe APL conventionnelle font appel à des symboliques simples; lorsquil sagit dalgèbre matricielle binaire (modulo 2), les symboles sont doubles : deux points, deux astérisques ...etc et font toujours partie des caractères ASCII que lon peut frapper sur nimporte quel clavier. En un quart de siècle dAPL, je nai jamais vu ** figurer dans aucune instruction. Quant au double point, il ninterfère pas le moins du monde avec la syntaxe APL dans laquelle son emploi était interdit. Le symbole : parfaitement récupérable si on nutilise jamais détiquettes mais de la programmation structurée, peut servir[13] pour obtenir la transformée cognitive dun objet dinformation quelconque (vecteur, matrice, hyper-matrice ...etc). La syntaxe est monadique. De même, le symbole .: monadique (deux caractères) définit la transformée hélicoïdale dun objet dinformation quelconque (vecteur, matrice, hyper-matrice ...etc). Le pariton[14] (matrice des intégrales successives) dune séquence binaire quelconque - un vecteur de bits - sobtient par le symbole monadique Œ: (deux caractères). Le géniton - cas particulier de pariton pour une séquence primordiale cest-à-dire un vecteur commençant par 1 suivi uniquement de zéros, sobtient par le double symbole __ (deux blancs soulignés successifs, de sorte que __N équivaut à Œ:N†1 ).
Autres fonctionnalités
Sous INTERP, un point dexclamation tout seul (niladique) reproduit sur lécran lensemble des instructions précédemment exécutées.
Sous INTERP, un point dinterrogation tout seul (niladique) reproduit sur lécran lensemble des substitutions et équivalences possibles - non APL à proprement parler - entre symboles ou groupes de symboles et les fonctions de la zone. (Attention : seules les fonctions décrites ici sont présentes dans la zone COCSE; les autres se trouvent dans la zone expérimentale COCRAY laquelle nest pas pour linstant disponible).
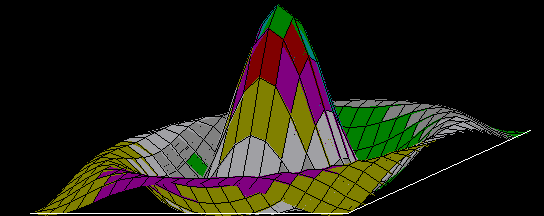
5. Le chapeau mexicain ou
Graphiques 3D:
½CHAPEAU2
109
CHAPEAU2
-8.1 8.1 0.8
-8.1 8.1 0.8
2 2 1÷2 2 2 1÷2
10×(SIN(((X)+(Y))))÷(((X)+(Y)))
La variable CHAPEAU2 est un vecteur de caractères éditable tel quel par léditeur APL. Les quatre lignes se lisent comme suit : pour X variant de -8.1 à 8.1 par pas de 0.8 et pour Y variant de -8.1 à 8.1 par pas de 0.8, calculer la formule ... etc, sachant quun potache non-APListe devrait comprendre quil sagit de la formule du chapeau mexicain, utilisée non seulement dans les livres de maths mais aussi en physique à propos de lélectrodynamique quantique. Pour le profane, on nutilise que les symboles APL, aussi présents sur toute bonne calculette, à savoir + - × ÷, les exponentielles étant exprimées sous forme... dexposants, et les fonctions habituelles de la trigonométrie par les abréviations fonctionnelles SIN , COS ... etc.
La syntaxe demploi est fort simple. Une instruction en langue naturelle telle que :
COURBE DE CHAPEAU2 va provoquer le calcul dun tableau de 22 lignes et de 22 colonnes (Z en fonction de X et de Y) avec apparition du message suivant :
dimension du Tableau : 22 22
j'ai compris :
10 mul (SIN(((X*2) plus (Y*2))*1 div 2)) div (((X*2) plus
(Y*2))*1 div 2 )
(ceci nétant que la transcription en APL de ce qui sexécute), puis du graphique (de type graphique G dans le cas présent).
Rappel : le graphique, tracé an APL*PLUS ou APL_SE est isotrope en fenêtre DOS. Après tracé, on passe en fenêtre « Windows » (non isotrope : les horizontales sont légèrement plus longues que les verticales, ce qui, en mathématiques na pas beaucoup dimportance tant quil sagit de graphes). Le graphique en couleurs est alors transféré - sans intervention daucun logiciel - directement dans un fichier « Word » bien quil soit en « bitmap » couleurs, comme un vulgaire caractère (par un couper-coller) :
La session APL en fenêtre « Windows » possède un petit carré gris à gauche de len-tête de la fenêtre. Il suffit de cliquer à la souris sur ce carré pour faire apparaître le menu « Edition », lequel a deux sous-options actives « Marque » et « Copie Entree ». Il suffit de relâcher le bouton de la souris sur « Marque » pour que lon puisse au curseur (toujours à laide de la souris), marquer - par un rectangle jaune - la partie à copier. Puis, par choix à la souris, de la sous-option « Copie Entree » du même menu « Edition », la partie sélectionnée de lécran graphique est sélectionnée - ceci se manifeste par un passage bref en video inverse; il ne reste plus quà changer dapplication pour coller au bon endroit, par exemple sous « Word6 » ledit graphique (commande <Ctrl> V). Si le graphique est inséré dans un tableau plus petit que lui, sa taille va sajuster automatiquement.
|
|
|
|
|
|
|
|
|
|
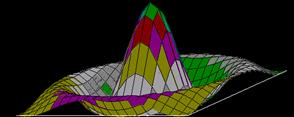
Voici ce que cela donne en plus petit : |
|
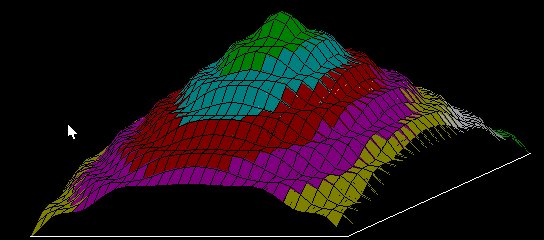
Les couleurs (arbitraires) dépendent de Z fonction de X et de Y. Les facettes rectangulaires sont triées en fonction de la profondeur, ce qui donne lordre du dessin et permet le recouvrement des parties cachées, selon lalgorithme du peintre.
’
COURBE ‘;‘‘;PARAMETRES
[1]
PARAMETRES„‘ ª ‘‘„0 ª
'‘‘„' if 0<ŒNC '' ª XYZ2 ‘‘
’
’
‘„DE ‘ fonction neutre
’
’
XYZ2 I;X;Y;Z
[1]
EFFACE ª Z„CREEXY ª '' ª DESSINE I
’
’
EFFACE fonction d’effacement de l’écran
[1]
ŒTCFF
’
’
R„CREEXY;b;D;d;E;L;M;N;P;T;V;Z;ŒIO;ŒELX
[1]
© ANALYSE LES 2 PREMIERES LIGNES DE
''PARAMETRES'': Xmin, Xmax, pas
[2]
© Ymin, Ymax, pas. PUIS CREE LES
VECTEURS X ET Y CORRESPONDANTS, PUIS
[3]
© RESULTAT: LE TABLEAU R=F(X,Y) DE
L'EXPRESSION DE LA 3ème LIGNE;
[4]
© X ou Y accolé à un nombre est lu comme
X ou Y à la puissance CE NOMBRE;
[5]
© 2
[6]
© Exemple: X ou (X2) est X au carré.
METTRE EXPLICITEMENT DES PARENTHESES
[7]
ŒIO„1 ª 'R„qR qBOX R' if
1=½½R„PARAMETRES ª L„½X„,ev R[1;]
[8]
L„3Ÿ.¬L,½Y„ev R[2;] ª b„'
' ª 'R„R[3;]' if~L„4ˆ1†½R
[9]
'D„b¬E„R[3;]ªR„R[4;]ªR[D/¼½R]„D/E'
if L ª V„X
[10]
–E„'M„1†1‡VªD„M-L„1†VªV„M˜L+P×V„0,¼1——D÷P„1†2‡V'
ª X„V ª V„Y
ª –E ª Y„V
[11]
L„R¹'XY' ª
L„1+L^1²R¹N„qD,'¯.' ª R„L/R
[12]
R„R qSSN
'ÐXXÐX*ÐYYÐY*',,4²'Ð',')','*',N,'Ð',')',[1.5]N
[13]
d„'EQUATION MAL ECRITE ou
PARAMETRES FOIREUX' ª ŒELX„'dª…'
[14]
ŒELX„'ŒDM'
[15]
E„R qSSN 'Ð+Ð plus Ð-Ð minus Ð×Ð
mul Ð÷Ð div '
[16]
METS 'J''ai compris:' EN VERT EN 11 0 ª
METS E EN JAUNE EN 12 0 ª R„–E
[17]
© fonctionne sur carte HERCULES ou EGA
[18]
© Essayer: COURBE CHAPEAU (ou CHAPEAU2)
’
’
R„ev B Cette fonction remplace - par ¯
[1]
R„qEA B qSSN '/-/¯'
’
’
„qEA ‘;ŒELX Cette fonction est une sorte d'Exécute si tu peux
[1]
ŒELX„'„Ð' ª
„–‘
’
’
‘R„‘A if ‘B;‘E;‘L;ŒELX
[1]
ŒELX„'ŒDM'
ª ‘L„‘B>0 ª ‘R„‘L/‘A ª
‘E„0¬1†0½‘R ª –‘E/‘R ª
–‘E/'‘R„0 0½‘R' ª
‘L„0<‘B„‘B-1 ª …‘L/1
’
’
METS B Mettre sur l'écran le message B
[1]
cMSG MSG B
’
’
C MSG B
[1]
Ð
ª W„pMSG,¯2† 0 1 ,ŒPW˜½B„•B ª W ŒWPUT B ª W
ŒWPUT C
’
’
DESSINE
I;A;B;C;c;D;d;E;e;F;G;H;i;J;j;K;k;L;l;M;m;N;n;O;P;p;Q;R;S;T;t;U;V;v;W;ŒIO;ŒELX
[1]
bon ª err ª ŒIO„1 ª
t„-1†1‡ŒAI ª © Résultat: temps consommé en secondes
[2]
F„800+100×her ª d„100-50×her ª
ERRG„'OK'
[3]
K„'Dimension du Tableau ',•D„½Z
ª METS K EN MAGENTA EN 4 0
[4]
Z„-,Z ª K„0,¼¯2+½X ª N„½Y ª
J„×/D ª Y„J½-Y ª bon ª T„Z,[1.5]Y
[5]
X„J½D[2]/X ª Eff 'Z Y' ª T„X,T ª Eff
'X' ª L„O,N+²O„2†E„4½¼3
[6]
L„L°.+0,¼¯2+N ª L„L°.+K×N ª
A„-±÷6 ª U„T+.×1²1´–ro‘ ª U[;3]„T[;3]
[7]
Eff 'T' ª A„±¯0.1 ª
U„U+.×2²2´–ro‘
[8]
T„˜šU ª D„0 ª
'U[;D]„U[;D]-T[D„D+1]' if 3 ª Eff 'T' ª U[;1]„U[;1]×3÷4
[9]
D„F÷—/—/U ª U„D×U ª
U„˜U ª U„d+U ª D„4,×/1‡½L ª L„D½L ª W„ 3 2
[10]
V„U[L;3] ª U„ 0 ¯1 ‡U ª
'L„L[;“+šV]' if I=1 ª L„³L ª j„÷3 ª ©I„0¬1†,I
[11]
c„ 1 3 , 2 2 ½²W ª
P„'gfinªrestec' ª i„'memecªinitg 1' ª A„0 ª Q„ 1 4 2
[12]
'p„''1ŒGLINE
TªŒAV[177]ŒGPAINT HªŒAV[220]ŒGPAINT Hª2ŒGLINE T''' if
her
[13]
'p„''1ŒGLINE Tª0ŒGPAINT
HªNŒGPAINT HªNŒGLINE lª0ŒGLINE t''' if ega
[14]
M„—/V„+/U[L;2] ª
H„¼K„8 ª H„H÷K ª D„²1,½V ª
C„D½1++/V°.>C+˜+H×M-C„˜/V
[15]
S„'T„Q½U[A„A+1;;]ªN„1+C[A;1]ªH„M[A;]ªl„T[;2
3;]ªt„T[;2 1 3;]ªp if mg'
[16]
C„1+C-7×8=C ª
G„'A„A+1ªN„C[A;1]ªA,,U[L[A;K];]ªN,¯1,M[A;]' ª 'G„S' if mg
[17]
'C[;]„1' if her^I<0 ª
B„'A<D' ª ŒELX„'ERRG„ŒDM' ª 'VXYZ2' if I=1
[18]
'i if mgªL„´L,L[;1]ªCŒGLINE
U[L;]ª15ŒGLINE 1 3 2½U[1,J-2†N-1;]' if I=¯1
[19]
e„'n„÷L„1—300˜˜3×—/|,vªL„nׯ1+¼LªG„½v„L°.×v[1;;]ªV„v+G½W'
[20]
m„'v„T[D˜K+1;;]-W„V„T[,K„K+1;;]ªe
if 0^.>,v[;;1]ªC[K;1]ŒGLINE Vª0ŒGLINE W'
[21]
'i if
mgªL„´L[;¼3]ªD„1†½T„U[L;]ªK„0ªm if Dªn„-N,¯3
¯2ª0ŒGLINE n†Tª15ŒGLINE 1 3 2½U[1,J-2†N-1;]' if I=0 ª
t„t+1†1‡ŒAI ª P if mg
’
’
VXYZ2;D;J;s;V
[1]
M„L[; 2 2 2 ½ 2 1 4 1 2 3 4 3] ª
M„-/[4]U[M;¼2]
[2]
D„²3,J„½s„|,M[;;1;]pv2 M[;;2;]
ª L„D½L[; 2 3 ½ 1 2 4 3 2 4]
[3]
Œ„D„+/V„Cte<s ª
s„V/s ª MM„Œ„s[10†“s] ª
U„U[L„VšL;¼2] ª C„Vš2šC
[4]
M„+/[2]U ª M„M÷3 ª M„M,1 ª i if
mg
[5]
S„'ŒDM' ª ERRG„'OK' ª
ŒELX„'ERRG„ŒDMªP if mgªŒELX„Sª…' ª G wh B
’
’
R„A pv2 B;Q Produit vectoriel de A par B
[1]
Q„¯1+½½A ª Q„Q½';' ª
–'R„-/A[',Q,'1 2]×B[',Q,'2 1]'
’
’
Eff ‘ Efface les variables devenues inutiles
[1]
‘„ŒEX ‘
’
’
bon Signal sonore indiquant que tout va bien
[1]
ŒSOUND 50 100
’
’
‘E wh ‘L;‘C Fonction "tant_que"
[1]
‘C„–•‘L
ª –‘C/‘E ª …‘C/1
’
’
err
[1]
ŒELX„ŒALX„'ŒDM' ª
ERREUR„'...OK...'
’
fonctions non listées ici :
initg fonction de début de graphique (initialise le
mode en fonction de la carte)
gfin fonction
de fin de graphique (restaure le mod « texte »)
memec fonction de mise en mémoire de l’écran de
texte
restec fonction de
restauration de l’écran de texte
qR qBOX R équivalent
de
ŒR
ŒBOX R en APL68000 : transforme R en vecteur si R est
une matrice de
caractères, et
réciproquement
ega variable (1 ou 0 si carte ega ou cga)
her variable (1 ou 0 si carte "Hercules"
ou non)
mg variable
(1 ou 0 selon que l'on désire des messages ou non)
Cte variable scalaire numérique (valant ici 100)
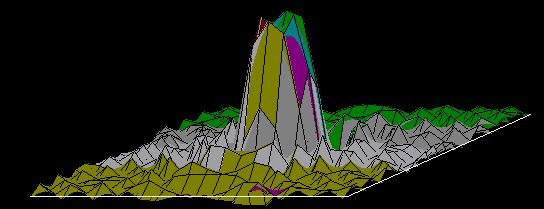
On peut proposer, à partir du chapeau mexicain, la variable AIGUILLE :
AIGUILLE
112
AIGUILLE
-8.1 8.1 0.8
-8.1 8.1 0.8
2 2 2 2
10×(SIN(((X )+(Y ))EXP .8))÷(((X )+(Y ))EXP .7)
de telle sorte que linstruction COURBE AIGUILLE donne limage suivante (relative à un paysage fractal quelque part au Nouveau Mexique ou dans le Colorado) :
|
|
’ R„A EXP B
[1]
cartes '*'
’
’
cartes ‘;;‘‘;
[1]
„'R„A°.',‘,' B' ª
„1=½½B ª ' if „^1=½½A' if
^‘‘„0<ŒNC 'A'
[2]
„‘‘/' A ' ª
„'R„',,‘,' B' ª if~
’
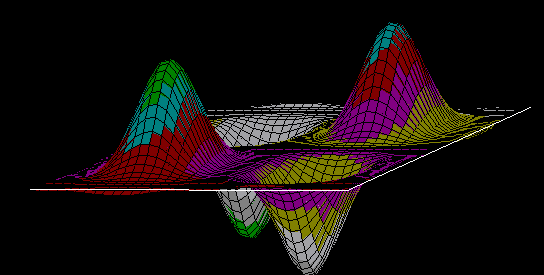
La fonction EXP est une simple exponentielle en produit extérieur. Toutefois, lutilisation de la sous-fonction cartes permet de généraliser le concept. Voici ce que lon obtient à partir de la variable PYR:
PYR (de
dimension 76 caractères, une pyramide Maya ?) :
-3
3 0.3
-3
3 0.3
2 2
¯0.4ט20×(EXP(-((X
)+(Y ))))×(X+Y)
|
|
On peut conserver en mémoire une foule déquations, en APL*PLUS
ou en APL_SE et ainsi explorer les fonctions Z=f(X,Y) à peu de frais. Exemple :
C3 Le
graophique a alors 36×71
soit 2556 points
-3.5
3.5 .2
-3.5
3.5 .1
3 3
3×((SIN X) )×((SIN
Y) )
|
|
C2
-30
30 2
-30
30 2
2 2 .5
-Z-SIN
Z„((X )+(Y ))
|
|
C1 seulement
661 points soit 31×21
-3
3 0.2
-3
3 0.3
2 2
-4×(EXP(-((X
)+(Y ))))×(X+Y)
|
|
par AFAPL
Vivek S. Borkar, Probability
Theory, an advanced couse, Springer New York (1995) ISBN 0-307-94558-X, 138
p.
Ouvrage court de Mathématiques pures, ultra-modernes.
D. C. Rapaport, The Art
of Molecular Dymamics Simulation, Cambridge University Press (UK) (1995)
ISBN 0-521-44561-2, 400 p.
Livre orienté vers lInformatique. Nombreux programmes de simulation en langage C.
Jean-Loup Chrétien, Sonate au clair de terre, Denoël, (1994) ISBN 2.207.24153.X, 230 p.
Général de réserve de lArmée de lair, Jean-Loup Chrétien est le premier spationaute français a être parti dans lespace. Un de ses coéquipiers sappelle Vladimir Djanibekov. Commandeur de la Légion dhonneur, cité à lordre du mérite et héros de lUnion Soviétique, il est aujourdhui directeur des astronautes du Centre national dEtudes spatiales.