Sur le calcul récurrent
en APL
par Andrei Bouzine
Introduction
It is known, that APL provides the possibility to
think global, in terms of arrays. It has
the powerful incorporated means of processing arrays as a whole. Unfortunately,
not all problems of array processing can be solved elegantly by APL. The APL is
oriented on regular array processing, which means that all elements are
processed similary. However from time to time the researcher who uses arrays
often, requires singular or recurrent array processing, in which
the algorithm of single element processing depends either on this element
itself or on the other elements of array.
As examples of
singular processing we can mention calculating of logarithm of numerical vector
or the derivation of piecewise-smooth function in points among which there are
the points of nondifferentiability. It is quite obvious, that the points, where
the function or operator is not defined, must be excluded from the processing.
APL does not make this, nor informs which element can't be processed:
µx„1 2 ¯3 4
DOMAIN ERROR
µx„1 2 ¯3 4
^
Meanwhile, the following result should be desirable:
0 0.6931471806 # 1.386294361
To obtain such a result we must use cycle, but cycle in any interpreter works
very slowly. It would be fine if this
cycle was programmed as the immanent part of the language, as in the case
of reduction, scan or each operator.
In this article
we shall discuss another type of irregular array processing, namely,
the
recurrent calculating of the elements of array.
We define the recurrent calculations as the step by step process of
vector elements calculating, which is organised in such a manner that the next,
i-th element x(i) is calculated as a
function of fixed numbers k of previous elements
x(i-1), x(i-2),..., x(i-k) of the same array and the first k elements are initially known.
Suppose, we must fill the numerical vector of N
elements in the following manner:
This vector is quite ordinary; its length and type of
elements are fixed. We can say that this is classical, FORTRAN's array. It is
sad that the powerful APL can't fill this array quickly. While calculating such
an array you are put into a dilemma: either to write in elegant APL-style (for
example by the aid of scan operator - see below), or in classic programming
style - by the aid of cycle construction.
In the first case you will have the concise expression, which will work very
slow. In the second case the calculations will be made more quickly, but
all advantages of APL will be missed:
your code will be as long as in FORTRAN, and the calculation time will be
longer. An interjacent variant exists: you can use recursive function and MEMO
operator (Geyer-Schulz Memoization) (thanks for John Scholes of DyadicLtd., who has told me about this
operator). We can save the time by this operator, but, firstly, the
construction will be rather complicated, and, secondly, WS FULL error will be
occurred even with little value of N.
On the other side, the problem is very simple for
classic programming because each element can be calculated through the foregoing
element by the recurrence relation:
, which is coded
by one cycle.
But the interpreter is an interpreter. If you use the
explicit cycle in APL, you must say honestly that it will calculate more longer
than compiled executive module. This fact deters many users from APL. Generally
speaking, the history of APL (and J) is the history of disposal from explicit
cycles. This was made successfully for some problems by hiding the cycles into
operators, such as reduction, scan, inner and outer product, each. The cycles
implicitly organised by interpreter during operators' execution can be
optimized and calculated in some cases
more quickly than the cycles, organised by C, for example.
As you see
below, the extension of operators' definition domain on any functions makes
possible to avoid many cycles, but only formally. For example, scan operator
applied to user function with dummy left argument permits to code the recurrent
filling of vector. The paradox is that scan operator works not in recurrent
manner and the elegance in this case is
the cause of enormous time increasing in culculations. Furthermore, the
standard definition of scan (ISO8485; thanks for John Scholes, who informed me
about this standard) makes the recurrent organization of scan operator
principally impossible!
Don't think that the example mentioned above is exotic
one. Below you can find out, that almost
all
solutions in computing mathematics are recurrent calculations. Moreover,
many mathematical models are described by recurrence relations (Fibonacci
numbers, continued fractions, manifold function superpositions, stochastic
Marcovian processes etc.)
If the recurrent calculations were realised into APL
interpreter, it would be a brilliant argument of its favour. Computing problems
can be coded in a pair lines and the calculation time will be not longer than
for compiled programmes. I don't see any principle difficulties for
encapsulation of such recurrent operator in APL: the structures used in
recurrent calculations are usually defined rigorously and it is not necessary
to distribute memory dynamically during the calculations.
The objective of this article is to discuss the introduction a new operator - recurrent operator - into APL.
Investigation of recurrent
calculation speed in APL
The author of this article had been solving many years
the following problems:
1.Compute the trajectories of solution of ordinary differential equations
system ;
2.Solve the system of algebraic equations 
;
3.Solve optimization problem (sometimes with restrictions)
.
4.
(sometimes - from a set of initial points 
) by the aid of
some rule 
, where
a is a set of parameters,
i - the iteration's number (in case of
k initial points you must use not 
,but 
instead) the sequence 
is obtained.
Such algorithms are programmed in APL by cycles, but
the organization of calculating can be different. To diminish the calculation
time we have analysed different methods of cycle organization by solving some
model problem.
Namely, we have build the trajectory of ordinary differential equation
by ordinary Eulers method with step in 1001 points. The right part of the model
problem was be chosen for the reasons of time of solution must be appreciable
and the solution itself must be known (the solution of this Cauchy problem is
).
The right part of equation, i.e. the function 
, was coded
separately; Eulers method was coded as a function (or as
an operator) with f as
an argument (operand).
Accumulation of resulting vector, which contains N+1
elements, can be realized as concatenating to it one number in one step, or as
filling the correspondent component of predefined vector. Experiments shown
that the second method is preferable in time (about 1.5 times; this result corresponds qualitatively with Robert Bernecky's one, see [8]).If organized recursively, the cycle works about 1.5
times slower; perhaps the transference of arguments is for APL the hard work. If we use
the operator instead
of the function, we can spare the time slightly (10-15 %% for our
task).
The cycle may be organized by branching (&) or by control
structure (:For...). The second way is more preferable in time, but not crucial
(about 15-20%% for our task).
The calculations was executed by DyalogAPL,v.7.2,
processor Intel486/66. The best time, namely, 0.8 sec. to calculate trajectory
of 1001 points, we have reached by the following method:
[0]
r„TN(f EuFor)x0;w;T;N;‘;i
[1]
T N„TN
©Final time and number of steps
[2]
‘„T£N
©Step
of integration
[3]
r„x0,N½0
©Empty yet
[4]
:For i :In ¼N
[5]
w„r[i]
[6]
r[i+1]„w+‘¢f
w
[7]
:EndFor
In modern APL this problem has an other, concise
solution:
F\(N+1)/x0
, where function
F is defined as follows:
[0]
r„dummy F x
[1]
r„x+‘¢f x
Here is a global variable, f is the function, coded
right part of differential equation. The function F - operand of scan operator
- must be dyadic, this is the reason why
we use the dummy left argument.
This elegant solution works, but takes 264 seconds! We encounter a paradox situation: while teaching APL as a most concise
programming language, we must keep back the fact that Euler method can be
programmed in five symbols and we must program the method in FORTRAN-manner.
The cause of slow work of scan operator is the fact,
that each component of result is calculated anew, not using the previous
components. The scan operator is foredoomed to such processing because
ISO-standard value of F\x is 
, and the (i-1)-th component in this expression is absent in
general case. Nevertheless, if F is independent of left argument and all
elements of initial array are equal to x0, then the value of i -th component of
F\x is equal to 
. This means that the i -th component can be calculated as a value
of function F of (i-1)-th component, that is recurrently.
It's easy to understand that we can code more complex
recurrent algorithms with the aid of scan operator, corresponding function F
and initial value x0. In these cases the result of each step may be not a
scalar, but more complex array, or the initial value may be a vector. For
example, in the last case the following expression is valid to calculate N
values 
starting from initial values x0=(
) and using
recurrent relation 
:
(1 x0),,N
¯1
F\N/:x0
,where F is
coded as
[0]
r„dummy F x
[1]
r„(1!x),f x
The calculation of Fibonacci numbers belongs to this
case (f‑+/).
What we said above, means that the recurrent
algorithms may be coded concisely in modern APL, without explicit cycles by
scan operator, BUT they works in this case
without using recurrence, not optimally.
While calculating the trajectory of differential
equation we apply some function F N times. To evaluate the time which is
required for N-times application of function F within implicit cycle,
programmed by primitive operator, we can use reduction: F/(N+1)/x0. This
expression takes 0.5 sec for our model task. 50 percent quicker than in the case
of explicit cycle. And 10 times shorter...
Computing mathematics is recurrent
calculations[1]
The most numerical methods are iteration processes or
recurrent calculations. You can see the corroboration in any textbook in computing mathematics, [1]
for example.
Distinction between iteration processes and recurrent calculations is conventional.
Commonly, the term "recurrent" is used if the calculations are
processed by virtue of analytic
relations, which define the next element (number or simple array) as a function
value of elements calculated previously. The elements of calculated sequence
are enumerated; their numbers are integer scalars or integer vectors. (The last
case is typical for numerical methods of solution of partial differential
equations). The result of recurrent calculations is commonly represented as
calculated sequence in whole; the calculations itself are carried out prefixed
times - until the element with appointed number will be calculated. Recurrent
calculations are typical for numerical solution of differential equation and
mathematical modelling.
Iteration processes usually have as a result only the
final value of some variable (which can be an array), not the whole sequence of
values of this variable. The relation between the next value and previous
values is defined as usually not
analytically, but algorithmically; sometimes by using many auxiliary
variables. The step of iteration may be recurrent calculations itself (for
example, it can be sweep method). The iteration processes are typical for
numerical solution of algebraic equations, optimal control and optimization
problems, linear algebra problems. Commonly, it is not known anew how many
times we will repeat the iterations, and the end of process is controlled by
fulfilment of some conditions.
Whereas any set of data can be present in APL as an
array and whereas each algorithm can be programmed as APL-function, so far
forth all iteration processes may be considered as recurrent calculations. We
shall mention hereinafter the iteration processes also as recurrent
calculations .
Any recurrent calculation is represented by one cycle[2]. One step of the cycle is the step of recurrent calculation. The loop body is defined by the mapping
(APL-function)
. The inital value of cycle index
i is equal to k+1.
The final value of cycle index is defined by the
specified halt criterions. Often this criterions are described as some
conditions for calculated values, not for cycle index. But, in this article we
shall consider only the last case[3].
In this case the number of steps N is known before the calculations. Two
variants are possible. The first case is we calculate the whole array element
by element; the second is we are interesting only in the last element. To
distinguish this two cases we shall assign the minus sign to the value N in the
second case.
Before the calculations the initial values
x(1),x(2),...,x(k) is known.
So, the recurrent calculation has following
characteristics: initial values, number of steps and algorithm F to calculate
the next element by the means of previous. This characteristics presents
naturally the arguments of recurrent calculation operator (or, simply,
recurrent operator). The operand is the function F, which describes the
algorithm F (i.e. one step of recurrent calculations or of iteration process);
the right argument is an array of two components: initial values and the number
of steps. The left argument, if present, contains the parameters of function F.
The recurrent operator must build automatically the cycle with index i by means of its right argument. Two operations are executed into the cycle: the real indexes i‑k, i‑k+1,...,i‑1 are calculated and, secondly, the next value x(i) is calculated by the function F with actual right argument - the
set , and (if necessary) with actual left argument, which is equal
to the left argument (or its modification) of recurrent operator.
Two important notes should be made about the
function's F parameters.
At first, function F can be without any parameter.
Therefore it is convenient to make left argument of recurrent operator optional
(of course, if it is possible for your
APL version).
Secondly, the function F itself can depend on the
value of i. We can't define the actual
value of this parameter before the cycle, because it depends on the cycle
organization, which will be build only during the recurrent operator's
processing. The dependence or independence F of i we must show in special
manner. We mean that it is convenient to reflect such dependence by the special
structure of left argument of recurrent operator. Namely, if the left argument
of recurrent operator is the nested scalar, then i is a component of actual
left argument of function F, otherwise the actual left argument of function F
does not contain i. If the actual value of left argument of recurrent
operator is represented by nested scalar, then the actual value of left
argument of function F within the cycle must be the nested vector with two
arguments - the parameters of function F itself and the number of cycle step.
We shall use the symbol "¬" for brevity as a name of recurrent operator.
Examples of numerical methods
Let us consider some numerical methods and write them
by means of our hypothetical recurrent operator.
Euler method with step , the number of calculated points N and initial point
x0 for solution of Cauchi problem of first order ordinary differential equation
with right part f may be programmed as follows:
EulerStep¬ x0 N
, where EulerStep is defined as follows function:
[0]
r„ EulerStep
x
[1]
r„x+×f x
(Here f is global defined function; you can, of
course, define EulerStep as operator with operand f and use derived function f
EulerStep instead; see examples below)
Using implicit Euler method we solve the equation 
in each step.
is usually used for the solution of this
equation. This
Solving inhomogenious differential equation
the independent
variable t is the argument of function f and the actual value of this argument
is
×i. It means, that function F depends of i; to show
this fact we must use the nested scalar[4] :,
as the left
argument of recurrent operator:
[0]
r„par EulerStep1 x;;i
[1]
i„par
[2]
r„x+×(×i)
f x
In this case recurrent operator on one's own must form
the actual value of two-component argument par taking the left argument of
recurrent operator as a first component and cycle index as a second component.
Numerical solution of Cauchi problem of second or more
order ordinary differential equation may be reduced to the solution of first
order differential equation system or to using of one-dimensional difference
scheme [1].
Euler method for solution of the system of homohenious
differential equations we can code by recurrent operator as follows:
EulerStep¬(:x0)N
Well-known revisions of Euler method are the methods
of Euler-Cauchi, of Runge-Kutta and of 
of the result refines by
means of iteration for k:
with initial values 
. If we establish
that the M‑th refinement is acceptable, then the Euler-Cauchi method to
solve first order homohenious ordinary differential equation may be coded by
means of the following recurrent operator:
M ECStep¬ x0 N
, where ECStep is the function of one Euler-Cauchi
step:
[0]
r„par ECStep x;;M
[1]
M„par
[2]
r„ x F2¬ (x (x+×f x))(-M)
, and F2 is one
step of refinement:
[0]
r„par F2 y;
[1]
x„par
[2]
r„x+0.5××+/f y
Adams method calculates the i-th point of the resulting trajectory using a rather complex relation [2,p.187], which contains the values of k previous points, integration step and the set of constants C. k is a parameter of Adams method; the first k points of trajectory must also be known before calculations. We may program the Adams method for solution of homogeneous first order ordinary differential equation with fixed initial values x0 (the vector of length k) and with vector of constants C as follows:
C AdamsStep¬ x0 N
To calculate the trajectory with integration step for Cauchi problem in the interval (0,T) for autonomous differential equation with delay
X = ò(X(t_τ))
if the first M points x0=x(),x(2),...,x(M), =t/M of the trajectory x(t) are known, we can use recurrent operator in the following manner:
f EulerTau ¬ x0 (T÷‑tau÷M)
, where f is right part function of differential
equation and EulerTau is operator processing one step of calculations:
[0]
r‑(f
EulerTau) x
[1]
r„œ(¯1†x)+‘¢f 1†x
by step using of recurrent relation 
, where 
is
an initial
approximation of the root. The number of steps is limited as usually by some
value N. If the method does not converge after N steps, then the method is
considered as nonconvergent, starting the initial approximation involved. N is
commonly not very large, about 10-20. The recurrent operator for solution of
algebraic equation by
a
f Newton1 df¬ x0 (-N)
, where f Newton1 df is a derived function, which
makes one step of
[0]
r‑a
(f Newton1 df) x
[1]
r‑x-a×(f x)÷df x
This problem is a special case of the problem of
solution of the algebraic equation system by
a
f NewtonN df
¬ (:x0)(-N)
, where f NewtonN df is a derived function, which
makes one step of many-dimensional Newton method for known vector-functions f
(left part of the system involved) and df (Jacobian-function of function f):
[0]
r‑a
(f NewtonN df) x
[1]
r‑x-a×(f x)}df x
If Jacobian is calculated numerically by means of some
derived function f Jacobian with parameters parJ, then the recurrent
operator can be used in following manner:
a parJ f NewtonN (f Jacobian)¬ (:x0)(-N)
It is known, that the numerical methods of
optimization and optimal control are iteration methods similar to
Bisection method for solution of algebraic equation
f(x)=0 in interval [a,b]
(0>f(a)×f(b)) may be programmed as follows:
0.5×+/f Twain¬(:a b)(-N)
, where derived function f Twain makes one step of the
method:
[0]
r„(f Twain)x;b
[1]
r„0.5¢+/x
[2]
r„(1+0<¢/f
b)œ(b„r(2œx))((1œx)r)
Numerical
integration methods use often orthogonal polynoms. The more popular one
(Legendre, Chebyshev, Laguerre and Hermite polynoms) can be calculated using
recurrent relations [3]. For example, the Legendre polynoms are calculated by
the formula
It is easy to write the values of N Legendre polynoms
in points x (which is a fixed numerical vector):
(::x) Legendre¬(x (0.5ׯ1+3×x*2))N
, where function "Legendre" is defined as
follows:
[0]
r„par Legendre y;x;i;P1;P2
[1]
x i„par
[2]
P2 P1‑y
[3]
r„((2-÷i)×x×P1)-(1-÷i)×P2
Function interpolation can be often reduced to the
problem of solution of linear systems with n-diagonal matrix. It is
advantageous in this case to use not the general algorithm of linear system
solution (}), but the sweep method. The sweep method is often
used also in other problems of computing mathematics[1]. This method calculates
the coefficient sequences {ai} and {bi}, so, that i-th component of linear system solution
can be calculated by means of the first component as 
. The coefficients
ai and
bi are calculated by using the elements of main
diagonal K, bottom diagonal L, upper diagonal M and the vector of right part b
of the system involved. To calculate the consequence
ai you can use the recurrent operator in following
manner:
alpha„(›b L K M)Falpha¬(0,b[1]£M[1])(½b)
, where
[0]
r„par Falpha a;b;L;K;M;i
[1]
b L K M i„par
[2]
i-„1
[3]
r„(b[i]-a+.¢iœ¤L
K)£M[i]
The consequence
bi is calculated similarly. Both sequences are used to calculate
the system solution. You will see below, that the solution of threediagonal
systems can be processed by this method much more quickly than by using
}.
In numerical methods of linear algebra the recurrent
calculations are used often too. For example, to reduce the matrix A to
Frobenius canonical form (which may be used to solve the eigen values problem),
we must execute n times the iteration 
, where Mn-i is calculated by matrix 
[2]. This method
may be realized by means of recurrent operator as follows:
(:n)Frob¬(:A)(-n‑1
½A)
, where
[0]
r„par Frob A;IM;ni;n
[1]
n„1œpar
[2]
ni„n+1-2œpar
[3]
IM„(¼n)°.=¼n
[4]
IM[ni;]„A[ni+1;]
[5]
r„IM+.¢A+.¢ŽIM
The numerical solution of partial differential
equations is commonly step by step calculations of layers in many-dimensional
net, starting from initial layer. The values of points of next layer are
related recurrently with the points in previous layers, this is called
difference scheme. Thus, the recurrent operator with difference scheme as
operand can calculate all layers of the net, realizing the numerical solution.
Each net layer is a simple numerical array with rank
equal to the problem's dimension minus one. Usually, the calculation of one
layer is the recurrent calculations[5].
Consider, for example, two methods of numerical
solution of mixed problem for parabolic type equation [1]
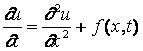in domain [0,X]×[0,T] with initial conditions 
and boundary conditions 
. We will search for the numerical solution 
in net points 
. Let us denote by U1 the set of known values {
, m=1,2,3,...,M}. Numerical solution of the problem involved
consist in consequently filling of matrix U with rank M×N, where the first column, the first and last row of
this matrix is known before calculations:
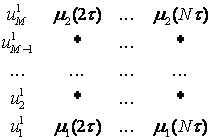We write the symbol "*" instead the elements
which must be calculated.
Usually the following difference schemes are used to
solve the problem:
(A)
(B)
(C)
In all three cases the numerical solution fill
consequently from left to right the columns of
The scheme (A) calculates each point of next column by
three adjacent points in previous column. For scheme (B) all points of next
column are the solution of three-diagonal linear system with coefficients
depending on all points in previous column and corresponding values of
m functions. The
difference scheme (C) is a generalization of schemes (A) and (B). If 0<s£1, then the way
to calculate the next column is the same as in scheme (B), but the coefficients
of linear system, which must be solved in each step, are the other. If 0=s the scheme (C)
is identical to scheme (A). Note, that
t,h and
s are the parameters of difference scheme using; values 
,
can be calculated if we know indexes m and n, as the result
of globally defined functions
j, m1,
m2 (Fi, Mu1, Mu2) correspondingly.
For the scheme (A) the problem is solved by recurrent
operator as follows:
(:(X÷N),(T÷M),M)ShA¬(:U1) N
,where U1 is the vector of initial points and ShA is the function, which describes one step
in the scheme (À):
[0]
r„par ShA u;h;tau;M;n;th;t
[1]
h tau M n„par
[2]
th„tau£h¢h
[3]
t„tau¢n-1
[4]
r„(Mu1
t),((›u)FA¤1+¼M-2),Mu2 t
, where function
FA is defined as
[0]
r‑x FA m
[1]
r‑x[m]+(th×1
¯2 1+.×x[m+¯1 0
1])+tau×Fi
(h×m-1)
(tau×n-2)
Note, that inside the function ShA, in function FA¨, the implicit
cycle is hidden, which will, probably, detain the calculations (in the case, if
it is realized in such a manner that it calls the function FA each times. It is
precisely repeating of these calls that may be cheated by many-dimensional
recurrent operator).
For difference scheme (B) the problem can be solved as
follows:
(:(X÷N),(T÷M),M)Sh¬(:U1) N
,where ShB is the function, which describes one step
in the scheme (B):
[0]
r„par ShB u;h;tau;M;n;ht;t;h2;b
[1]
h tau M n„par
[2]
ht„(h¢h)£tau
[3]
t„tau¢n-1
[4]
b„-(ht¢¯1‡1‡u)+(h¢h¢Fi¤(h¢¼M-2),¤t)
[5]
b[1]-„Mu1
t ª b[M-2]-„Mu2 t
[6]
r„((M-2)½-2+ht)((M-3)½1)((M-3)½1)Solve3D b
[7]
r„(Mu1
t),r,Mu2 t
, where Solve3D is the function, which solves the
corresponding three-diagonal linear system of rank (M-2)×(M-2). This
function calls the other functions Fi, Mu1, Mu2 and can contain the recurrent
operators (see above).
Other examples of onedimensional
recurrent problems
The problem of recurrent filling of an array,
formulated in introduction of this article, can be solved as follows:
(›«)Sqr100¬10 100
,where
Sqr100 is "one-step"
function:
[0]
r„i Sqr100 x
[1]
©Function for reccurent calc of complex root
[2]
r„(x+101-œi)*0.5
This problem is actually the problem of calculation of
complex function superpositions; the other example is
We can use the recurrent operator to calculate this
superposition:
1°±¬(1±x)n
(Here we use composition operator
°. If your
interpreter does not afford the composition operator, you must write the name
of sine function, programmed manually, instead 1°±).
Some mathematical models brings forth the recurrent
calculations, which result in continued fraction[5]. Continued fraction in
general form
may be programmed by recurrent operator as follows:
((›a b)Chain¬(a[1],b[2]+¢/a[1 2])(-n))
£((›a b)Chain¬ (1,a[2])(-n))
,where a,b are the fixed sets {an},{ bn ; b1 =1}, and
function Chain describes one step of recurrent calculations (see [5], p.811):
[0]
r„par Chain x;a;b;i
[1]
a b i„par
[2]
r„(b[i]¢x[1])+a[i]¢x[2]
In particular cases the continued fractions are
programmed more simply.
It is easy to program the discrete Marcovian
stochastic processes [6] by means of recurrent operator. Really, the
probability distribution at the moment involved
is defined only by fixed set of previous states of such processes. (We
can say, that discrete Marcovian processes are
stochastic generalization of recurrent relations).
Here is one example of Marcovian process:
?¬1000 100
Another example is the Marcovian chain of length n with 10 states, transition matrix P and initial state x0:
P
Marcov¬x0 n
, where
[0]
r„P Marcov x;p
[1]
©Marcovian transition
[2]
p„+\P[x;]
[3]
r„1++/p°.<0.000001¢?1000000
Onedimensional recurrent operator
Hereinafter is the DyalogAPL text of recurrent
operator[6]. It
checks the correctness of right argument (line 3), prints the result if the
number of steps is not more than the length of initial values' vector (line 8),
construct the actual left argument of F function, which will be used into the
cycle (lines 9-15) and apply the cycle to fill the resulting array (lines
18-24) or to calculate the value in the last iteration (lines 25-32).
[0]
Y„{parF}(F
RecIt)R;r;s;w;K;I;i;num;p;X;left;N;argF
[1]
©Onedimensional operator for reccurrent calculations
[2]
©and for iteration steps (Andrei Buzin 09 April 1997)
[3]
–((,2)»½R)/'''Right
argument must be a vector of 2 elements!''ªY„«ª…0'
[4]
X N„R
©Initial values,Number of steps
[5] ©N must be simple integer (N<0 for iterations, N>0 for recurrence)
[6]
K„½X„,X
©Number
of initial values
[7]
…(K<|N)/l10
©Is the
result yet ready?
[8]
Y„–(1+N‰0)œ'(-N)œX'
'N†X' ª …0
[9]
l10: :If 0=ŒNC'parF' ©Prepare the left arg of F
[10]
left„''
[11]:ElseIf
(0=½½parF)^1<|parF ©If parF is a nested scalar
[12]
left„'((œparF),i)'
[13]:Else
©In other cases
[14]
left„'parF'
[15]:EndIf
[16]
©CYCLE
[17]…(N<0)/iTER
[18]Y„N†X
©For pure
recurrence
[19]i„K
[20]lR:…(N<i„i+1)/0
[21]num„²i-¼K ©effective
elements
[22]–(1=½argF„Y[num])/'argF„œargF'
[23]Y[i]„›–left,'
F argF'
[24]…lR
[25]iTER:Y„X
©For
iterations
[26]i„K
ª N„-N
[27]lI:…(N<i„i+1)/eI
[28]–(1=½argF„Y)/'argF„œargF'
[29]Y,„›–left,'
F argF'
[30]Y‡¥„1
[31]…lI
[32]eI:Y„œ¯1†Y
Now let us see
the work of our recurrent operator:
1.
USING EXPLICIT RECURRENT FORMULA
1.1.
10 Fibonacci numbers, Two initials:
©COMMENT
+/RecIt(1
1)10
©EXPRESSION
1 1 2 3 5 8 13 21 34 55
©RESULT
1.2.
10 Fibonacci numbers, Three initials:
+/RecIt(1
1 1)10
1 1 1 3 5 9 17 31 57 105
1.3.
50-th Fibonacci number
+/RecIt(1
1)¯50
1.258626903E10
1.4.
Sequence a,1/a,a,1/a,....
a„2ªN„10ª
£ RecIt a N
2 0.5 2 0.5 2 0.5 2 0.5 2 0.5
1.5.
Complex Root:sqr(1+sqr(2+...99+sqr(100)...);
(›«)Sqr100
RecIt 10 ¯100
1.757932757
1.6.
Sequence of complex Roots
2•(›«)Sqr100
RecIt 10 100
10.00 10.44 10.41 10.36 10.31 10.26 10.21 10.16 10.11 10.06 10.00 9.95
9.9
0 9.84 9.79 9.74 9.68 9.63 9.57 9.52 9.46 9.41
9.35 9.29 9.24 9.18 9.
12 9.06 9.00 8.94 8.89 8.83 8.77 8.70 8.64
8.58 8.52 8.46 8.39 8.33 8
.27 8.20 8.14 8.07 8.00 7.94 7.87 7.80 7.73
7.66 7.59 7.52 7.45 7.38
7.31 7.23 7.16 7.08 7.01 6.93 6.85 6.77 6.69
6.61 6.53 6.44 6.36 6.27
6.19
6.10 6.01 5.92 5.82 5.73 5.63 5.53 5.43 5.33 5.23 5.12 5.01 4.9
0 4.79 4.67 4.55 4.42 4.29 4.16 4.02 3.88 3.72
3.57 3.40 3.23 3.04 2.
84 2.61 2.37 2.09 1.76
1.7.
Complex sinus in point Pi/2: Pi/2+sin(Pi/2)+sin(sin(Pi/2))+...; recurrent
formula is X(i)=sin(X(i-1))
+/
1°±
RecIt (±.5)10
7.633368902
1.8. Complex
sinus in points Pi/4,Pi/2,...
3•+š†
1°± RecIt (›±.25¢¼5)10
5.783 7.633 7.354
3.142 ¯1.071
1.9.
Golden Ratio!
1°+°£
RecIt 1 ¯40
1.618033989
1.10.
Chain fraction 1/(1+1/(3+1/(5+...+1/103)...)
(›«)
Chain1 RecIt (£103) ¯52
0.761594156
1.11.Chain
fraction in general form: a0+b1/(a1+b2/(a2+....+bN/aN)...)
N„52ªa„0,¯1+2¢¼Nªb„(N+1)½1
((›a
b)Chain RecIt (a[1],b[2]+¢/a[1 2])(-N))£((›a b)Chain RecIt (1,a[2])(-N))
0.761594156
1.12.
5 first Legendre Polinoms in points x= 0
1 2
(››x)
Legendre RecIt (x(.5¢¯1+3¢x*2))5
0 1 2 ¯0.5 1 5.5 0 1 17 0.375 1 55.375 0 1 185.75
2.
NUMERICAL SOLUTION of EQUATIONS
2.1.Newton
Method of solution of eq. F2(x)=x*2-1=0 with explicit calculated derivation
DF2, initial point x=2, 10 steps:
F2
NewtonN DF2 RecIt 2 ¯10
1
2.2.Newton
method of solution of eq. F2(x)=x*2-1=0 with indirect calculated derivation by
Jacobian operator with step 0.0001:
F2
NewtonN (0.0001 Jacobian F2) RecIt 2 ¯10
1
2.3.Illustration
of convergency:
F2
NewtonN (0.0001 Jacobian F2) RecIt 2 10
2 1.25001875 1.025012375 1.000306381 1.000000062 1 1 1 1 1
2.4.Newton
Method of solution of Thomson system (,v.25#1)
with numerical calculated derivation with step 0.0001:
Thom
NewtonN (0.0001 Jacobian Thom)RecIt
(›1 1 1)¯10
0.8779657603 0.6767569705 1.330855412
2.5.Twain
method of solution equation F2(x)=0:
0.5¢+/F2
Twain RecIt (›0 2)¯10
1.001953125
2.6.Solution
of threediagonals linear system 1 7 0
1
7 8
8¢X=2
0 9 3 3
(The
function Solve3D contains two calls of RecIt).
(1 8
3)(7 9)(7 8)Solve3D 1 2 3
¯0.4 0.2 0.4
3.
SOLUTION OF ORDINARY DIFFERENTIAL EQUATIONS (Cauchi problem)
3.1.
Explicit Euler solution of diff.eq. with right part 1-(sin(x))*2 Initial value=0, step .01. The result is x(t) in
points 0,0.01,0.02,...,0.99
3•0.01
RP EulerE RecIt 0 100
0.000 0.010 0.020 0.030 0.040
0.050 0.060 0.070 0.080 0.090 0.100 0.110 0.
119 0.129 0.139 0.149 0.159 0.169 0.178 0.188
0.198 0.207 0.217 0.226
0.236
0.245 0.255 0.264 0.273 0.283 0.292 0.301 0.310 0.319 0.328 0.
337 0.346 0.355 0.364 0.372 0.381 0.390 0.398
0.407 0.415 0.424 0.432
0.440
0.448 0.456 0.465 0.473 0.480 0.488 0.496 0.504 0.512 0.519 0.
527 0.534 0.542 0.549 0.556 0.563 0.571 0.578
0.585 0.592 0.598 0.605
0.612
0.619 0.625 0.632 0.638 0.645 0.651 0.658 0.664 0.670 0.676 0.
682 0.688 0.694 0.700 0.706 0.712 0.718 0.723
0.729 0.734 0.740 0.745
0.751
0.756 0.761 0.767 0.772 0.777 0.782
3.2.
Implicit Euler solution of this problem. Number of steps to find root in one
Euler step is equal to 5
3•0.01
5 RP EulerI RecIt 0 100
0.000 0.010 0.020 0.030 0.040 0.050 0.060 0.070
0.080 0.090 0.100 0.109 0.
119
0.129 0.139 0.149 0.159 0.168 0.178 0.188 0.197 0.207 0.216 0.226
0.235 0.245 0.254 0.263 0.273 0.282 0.291
0.300 0.309 0.318 0.327 0.
336
0.345 0.354 0.363 0.371 0.380 0.388 0.397 0.405 0.414 0.422 0.430
0.439 0.447 0.455 0.463 0.471 0.479 0.486
0.494 0.502 0.509 0.517 0.
524
0.532 0.539 0.547 0.554 0.561 0.568 0.575 0.582 0.589 0.596 0.603
0.609 0.616 0.623 0.629 0.636 0.642 0.648
0.655 0.661 0.667 0.673 0.
679
0.685 0.691 0.697 0.703 0.709 0.714 0.720 0.726 0.731 0.737 0.742
0.747 0.753 0.758 0.763 0.768 0.774 0.779
3.3.
Explicit Euler to solve nonhomogenious equation dx/dt=f(x,t),x(a)=x0,
t=a,a+‘,...,a+N‘.
Let
f=(x*2)-6/(t*2)
‘„.05 ª a„1 ª x0„2 ª
N„10 ª
6•(›‘
a) Mon9_6 EulerT RecIt x0 N
2.000000 1.900000
1.808391 1.723971 1.645732 1.572820 1.504508 1.440171 1.
379267 1.321324
3.4.
Runge-Kutta method of solution
6•(›‘
a) Mon9_6 RungeKutta RecIt x0 N
2.000000 1.904761 1.818179
1.739127 1.666662 1.599994 1.538454 1.481473 1.
428561 1.379298
3.5.
Euler method to solve homohenious equation with delay
dx/dt=-x(t-Tau); x(t)=cos t ,if 0ˆtˆTau
F„2°± ª ‘„.01 ª Tau„1.57
ª 'x(3.14)='(‘ ‑ EulerD RecIt (F ‘¢¯1+¼—Tau£‘)¯314)
x(3.14)=
¯0.9941912509
4.
SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS
4.1. Parabolic Equation(PPE Problem). Explicit Scheme.
du(x,t)/dt=d2u(x,t)/dx2+(x*2-2t);0ˆxˆX;0ˆtˆT;
u(x,0)=U1(x);u(0,t)= Mu1(t);u(X,t)= Mu2(t);net
(h,tau)
h„.1 ª tau„.005 ª X„1 ª T„.02
ª N„—1+T£tau ª M„—1+X£h ª U1„M½0
³²†(›h tau M)ShA RecIt(›U1)N
0 0.005 0.01 0.015
0.02
0 0.00405 0.0081 0.01215 0.0162
0 0.0032 0.0064 0.0096 0.0128
0 0.00245 0.0049 0.00735 0.0098
0 0.0018 0.0036 0.0054 0.0072
0 0.00125 0.0025 0.00375 0.005
0 0.0008 0.0016 0.0024 0.0032
0 0.00045 0.0009 0.00135 0.0018
0 0.0002 0.0004 0.0006 0.0008
0 0.00005 0.0001 0.00015 0.0002
0 0
0 0 0
4.2.
Solution PPE Problem by Implicit Scheme.
h„.1 ª
tau„.005 ª X„1 ª T„.02 ª N„—1+T£tau ª M„—1+X£h
ª U1„M½0
³²†(›h
tau M)ShB RecIt(›U1)N
0 0.005 0.01 0.015
0.02
0 0.00405 0.0081 0.01215 0.0162
0 0.0032 0.0064 0.0096 0.0128
0 0.00245 0.0049 0.00735 0.0098
0 0.0018 0.0036 0.0054 0.0072
0 0.00125 0.0025 0.00375 0.005
0 0.0008 0.0016 0.0024 0.0032
0 0.00045 0.0009 0.00135 0.0018
0 0.0002 0.0004 0.0006 0.0008
0 0.00005 0.0001 0.00015 0.0002
0 0 0 0 0
5. LINEAR
ALGEBRA
5.1.Frobenius
form of matrix A= 5 6 1
8 8 4
2 9 5
2•(›n)Frob
RecIt (›A)(-n„1†½A)
18.00 ¯19.00 ¯116.00
1.00 0.00
0.00
0.00 1.00
0.00
6.
STOCHASTIC PROCESSES
6.1.
Marcovian Process with absorb state 1:
?
RecIt 1000 20
1000 353 102 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
6.2.
Marcovian Chain with transition matrix P (10 states):
P
Marcov RecIt 5 100
5 10 2 2 6 5 3 1 1 2 3 3 8 2 1 2 8 6 4 10 10 8 3 3 9 7 8 7 5 1 6 5 3 1 3
3
10 6 9 4 4 10 8 7 9 9 10 8 3 1 8 6 9 7 2 2 2 3
6 5 2 4 10 8 6 4 5 9
9 6 9 6 6 9 8 1 2 3 9 7 9 7 7 5 7 8 4 4 5 10 2
3 6 4 7 5 10 2 2 3
6.3.
Birth and Death Process with Poisson distribution
1.15
10 BornDead RecIt 2 20
2 3 3 3 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
6.4.
Branching Process
3
Branching RecIt (›1 1 1)50
1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1
7.
OTHER INTERESTING APPLICATIONS
7.1.
Calculation of function F in points X with substitution by # if the result is
not defined
Let X=1
0 ¯2 3, F(x)=ln(x)
(››X)
µ Calc RecIt « (œ½,X)
0 ## 1.098612289
7.2.
Make Binary Tree of Height N with '*' in cells
N„5 ª †2°½°› RecIt (›,'*') N
*
*
*
* * * *
* *
* *
* * * *
* * * * * * * * * * * * * * * *
Of course, our recurrent operator works a little slower
than the cycle, which may be written for a concrete problem. Nevertheless, it
works more quicker than scan operator (see above).
It works with the same speed as recursion (if the
recursion is possible), but uses more less memory. For example, the problem
described in introduction (complex root) can not be solved by means of
recursion if N=25000 and 2Mb of memory ordered for workspace (WS FULL error);
our operator solves this problem in 47 seconds.
One illustration of effective work of our operator is the
calculation of 100 Legendre polynoms in 100 points. Below you can see the
graphs of first five and the hundredth Legendre polynoms, calculated by our
RecIt operator and drawn by GRAN (the system of interactive graph plotting in
APL [4]). To plot this graphs we must write only the function
"Legendre" (see above) and use the expressions x‑0.01×¼100 and
(:›x) Legendre RecIt (x(.5¢¯1+3¢x*2))100
to define graphs. The calculation of 100 polynoms in 100 points takes about one
second by my Intel486.
Another example of effective using of recurrent
operator is the solution of large linear systems with three-diagonal matrix
(see above). Our operator works significantly quickly in comparison with
function
} (this is because the main algorithm is quadratic, but
sweep algorithm is linear). The system with 250 variables can be solved in 31
sec. by
} function and in 3 sec. by our operator.
I have already noted that, if the recurrent operator
will be coded as primitive APL-operator, then we can spare about 30-40%% in
time versus our RecIt operator.
I see it is the time.
Bibliography
[1]N.S.Bachvalov, N.P.Zhidkov, G.M.Kobelkov
"Numerical methods", 1987 (in Russian)
[2]P.I.Monastyrski(editor) "Tutorial in calculation
methods", 1994 (in Russian)
[3]G.A.Korn, T.M.Korn "Mathematical
Handbook" (Russian edition 1974)
[4]A.Ju.Buzin, I.G.Pospelov "GRAN: an interactive
system of graphs' plotting", 1994 (in Russian)
[5]"Mathematical Encyclopedia", v.5, 1985
(in Russian)
[6]W.Feller "An Introduction to Probability
Theory and its Applications" (Russian edition 1984)
[7] N. Thompson "Applying Matrix Divide in
APL and J",APL Quote Quad,v.25#1,Sep. 1994,pp.211-220
[8]R.Bernecky "Strategies for Optimizing the API
Problem", Vector, v.13#4,April 1997,pp.7-10.
[9]A.Buzin "About recurrent calculations in
APL", APL¨Club, v.2#1,1997, pp.10-24.