Deux devinettes

DIVERSES APPLICATIONS DES PROGRAMMES DE GEOMETRIE MOLECULAIRE DE GERARD LANGLET

Claude Chachaty

Parmi les contributions majeures de Gérard Langlet à la physico-chimie figurent ses logiciels pour la représentation spatiale des molécules à partir de données cristallographiques (1). J'ai eu la chance de pouvoir bénéficier de la rare compétence de Gérard dans ce domaine alors j'avais depuis peu la responsabilité du laboratoire de Résonance Magnétique Nucléaire (RMN) et de Résonance Paramagnétique Electronique (RPE) du C.E.A Saclay. L'un des problèmes majeurs était en effet de disposer rapidement de logiciels pour l'exploitation des données expérimentales. Pour faciliter l'utilisation de ses programmes et nous apprendre à en créer d'autres, Gérard a donné en 1978 des cours d'initiation à APL .Ces cours ont été suivis avec un tel enthousiasme par les chercheurs du laboratoire, que nous avons adopté APL comme unique langage de programmation jusqu'au début de cette décennie en dépit de quelques limitations techniques qui n'existent plus aujourd'hui.

Le but de ma collaboration avec Gérard était de créer des programmes APL pour déterminer à partir de données expérimentales de RMN, les vitesse de réorientation des molécules en solution, leurs conformations préférentielles et les vitesses d'échange entre ces conformations. Pour mieux comprendre la nature de ces problèmes, il me semble nécessaire de mentionner au préalable quelques notions de base.

Les noyaux atomiques possèdent pour la plupart un moment magnétique associé à leur spin et sont donc assimilables à des aimants microscopiques qui interagissent à courte distance par l'intermédiaire des liaisons chimiques (couplage scalaire J) ou à longue distance à travers l'espace (couplage dipolaire D). La circulation des électrons dans le champ magnétique statique d'un spectromètre de RMN génère par ailleurs un champ de sens opposé qui s'exerce sur les spins nucléaires et déplace les raies de résonance (déplacement diamagnétique s). Le couplage dipolaire entre deux noyaux i et j est de la forme :

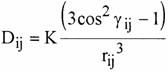[1]

où est l'angle entre le vecteur joignant les deux noyaux et le grand axe de la molécule assimilée à un ellipsoïde et K, une constante dépendant de la nature des noyaux. Alors que les paramètres J et s sont directement mesurables sur le spectre de RMN, les couplages dipolaires qui contiennent l'essentiel des informations sur la géometrie moléculaire, ne peuvent être obtenus dans les liquides que par des expériences de relaxation nucléaire. L'expérience de relaxation la plus courante consiste à mesurer le temps de relaxation longitudinale T₁ qui est la constante de temps d'alignement sur la direction de , de l'aimantation nucléaire macroscopique résultant d'un ensemble de moments magnétiques nucléaires . Dans le cas le plus simple d'une molécule rigide quasi-sphérique en réorientation rapide, la vitesse de relaxation d'un noyau i en interaction dipolaire avec des noyaux j prend la simple forme :

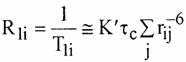[2]

où est le temps de corrélation qui correspond à peu prés à la durée moyenne de rotation de 30° d'une molécule.

En général, les molécules organiques en solution ont plusieurs conformations, certaines pouvant posséder un très grand nombre d'isomères rotationnels. On verra que les traitements informatiques des résultats experimentaux valables pour ces dernières que nous qualifierons de flexibles, diffèrent notablement de ceux applicables aux molécules semi-rigides où les rotations internes ne s'effectuent qu'autour de deux ou trois liaisons.

Notre première étude commune concernait les conformations de molécules semi-rigides comme les nucléotides, en particulier l'adénosine 5' monophosphate (AMP). Le problème nous avait été posé par une équipe de l'Institut Pasteur de déterminer le changement de conformation de ce nucléotide lorsqu'il se fixe sur le site récepteur d'une enzyme, la phosphorylase b, dont il est activateur (2). L'AMP comporte un cycle ribose lié à la base adénine composée d'un cycle pentagonal et d'un cycle hexagonal et à un groupe phosphate (figure 1). Les probabilités des deux conformères N et S du cycle ribose et des trois rotamères du groupe phosphate se déduisent simplement des couplages J entre protons vicinaux. Il n'existe par contre aucun couplage J entre les protons du cycle adénine et ceux du cycle ribose de sorte que les orientations relatives des deux cycles ne peuvent être déduites que des vitesses de relaxation de ces protons qui dépendent de leurs distances mutuelles (equ. 2).

Ce problème a été résolu grâce au système GEOMOL de Gérard, un groupe de programmes qui permet de calculer ab initio ou à partir de données cristallographiques, les coordonnées atomiques pour n'importe quelle conformation en choisissant les angles de torsion entre différentes liaisons. Le programme FIG de ce groupe dessine les formes moléculaires produites, avec éventuellement des effets de perspective comme sur la figure 1 ou la représentation des atomes par des sphères dont le rayon correspond à leur distance minimale d'approche (rayon de Van der Waals).

Pour déterminer les conformations les plus probables de l'AMP on calcule tout d'abord les distances entre un proton isolé de la base et les trois protons les plus proches du cycle ribose en fonction de l'angle de rotation Y autour de leur liaison commune.

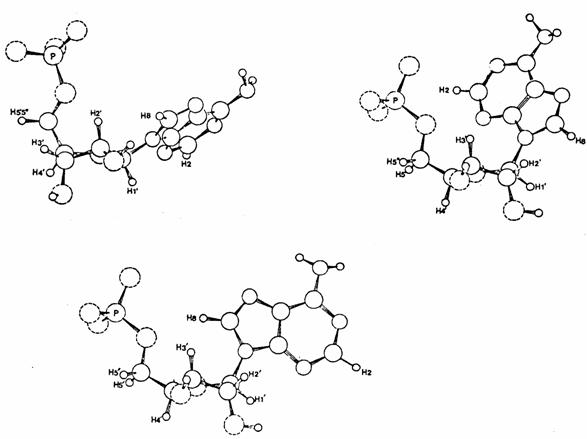
Figure 1. Conformères préferentiels de l'adénosine 5' monophosphate représentés comme pour les figures suivantes, à l'aide du programme FIG de Gérard Langlet.

Les deux valeurs les plus probables et de Y associées aux formes N et S du cycle ribose correspondent à l'écart-type minimum entre les vitesses de relaxation expérimentales et celles calculées par un programme annexe utilisant la relation [2] pour les quatre protons en question. Cette méthode est décrite en détail dans les références 3 et 4.

Au moment où ce travail a été effectué, nous ne disposions que de zones de 80 Ko. Le tour de force de Gérard Langlet a été d'écrire des programmes très performants et d'utilisation assez simple, dans un espace aussi réduit.

A partir de 1980, notre collaboration a porté plus particulièrement sur l'étude de molécules flexibles comportant généralement une chaîne hydrocarbonée. Il s'agissait de molécules utilisables pour l'extraction d'ions métalliques et dont certaines sont des agents tensioactifs formant des micelles et des cristaux liquides.

Selon le modèle d'isomérie rotationnelle de Flory (5), chaque groupe de trois liaisons successives d'une telle molécule, posséde trois rotamères : trans (T), gauche+ (G) et gauche- (g) représentés sur la figure 2.

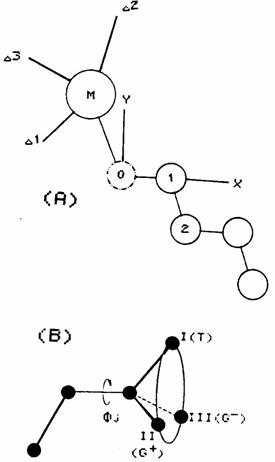
Figure 2. (A) Système de référence moléculaire. Dans ce référentiel, seuls les atomes 0 et 1 de la chaîne sont fixes, M est un ion métallique dans un complexe de coordination ou l'atome central de la tête polaire d'une molécule tensioactive. Les axes forment un référentiel secondaire choisi en fonction système étudié. (B) Définition des rotamères autour d'une liaison de la chaîne.

Pour une chaîne à N atomes, le plus souvent des carbones, il existe donc potentiellement ou conformères selon que l'on prend ou non en compte l'atome M auquel est lié la chaîne, dont certains sont interdits stériquement. Comme dans le cas précédent, le calcul des vitesses de relaxation ou des déplacement des raies de résonance nucléaires nécessite au préalable celui des coordonnées des atomes dans un système de référence moléculaire pour toutes les conformations permises. Dans ce but Gérard Langlet a écrit le programme CONSTRUC, remarquablement facile à utiliser. Chaque atome d'une chaîne étant désigné selon sa nature par une lettre, on définit tout d'abord les longueurs des liaisons entre les atomes et les angles entre deux liaisons successives. Pour générer les coordonnées des atomes, il suffit d'entrer ensuite leur séquence dans la chaîne comme le montre l'exemple le plus simple d'une chaîne à quatre atomes, celle de la propylamine :

CHAINE? NCCC

ATOMES : N C C C

NUMEROS : 0 1 2 3

ANGLES : 120.00 ¯110.00

LIAISONS : 1.40 1.53 1.53

TAPER 1 POUR CHI STANDARD (0 120 ¯120)

COORDONNEES : RESULTAT DANS TAB1. DIMENSION : 14 3

CHI (c) est l'angle entre les plans N-3, N-2, N-1 et N-2, N-1, N formés par les atomes. Les résultats de CONSTRUC sont regroupés dans le tableau :

Tableau 1

Atomes Conformations Coordonnées

x y z

0 0.00 0.0000 0.000

1 1.40 0.0000 0.000

2 T 2.17 ¯1.3250 0.000

2 G 2.17 0.6625 1.148

2 g 2.17 0.6625 ¯1.148

3 TT 3.67 ¯1.0593 0.000

3 GT 3.67 0.5297 0.917

3 gT 3.67 0.5297 ¯0.917

3 TG 1.80 ¯2.1376 ¯1.245

3 GG 1.80 ¯0.0095 2.474

3 gG 1.80 2.1471 ¯1.229

3 Tg 1.80 ¯2.1376 1.245

3 Gg 1.80 2.1471 1.229

3 gg 1.80 ¯0.0095 ¯2.474

Le programme CONSTRUC ne donne que les coordonnées des atomes constituant la chaîne. Celles des atomes "périphériques" tels que les hydrogènes d'une chaîne hydrocarbonée, s'en déduisent par des opérations simples.

Dans le référentiel x,y,z de la figure 2, les trois positions possibles pour l'atome 2 correspondent aux rotamères T, G et g de la séquence des atomes M, 0, 1, 2;

le nombre de positions que peut occuper le dernier atome de la chaîne est égal au nombre de conformations de celle-ci, soit 9 pour l'exemple du tableau 1. Dans ce tableau, les coordonnées ont été calculées pour l'option 1 du programme, valable pour une géométrie standard avec c = 0, 120°, -120° autour de chaque liaison. L'option ¹1 permet de choisir pour n'importe quelle liaison c = a, a+b, a-b, a etb étant des angles quelconques. Avec cette seconde option, il devient possible de construire pratiquement toute molécule linéaire avec comme seule limite un nombre de conformations compatible avec la taille de la zone de travail. Pour une zone de 15 Mo, cette limite se situe entre 300 et 500 selon le problème étudié.

Toutes les observables RMN que nous nous proposons de calculer (déplacement diamagnétique ou paramagnétique, vitesses de relaxation) sont du type dipolaire et dépendent linéairement de termes en , où D est de la forme de la relation [1]. Ce sont des moyennes pondérées par les probabilités des conformations que l'on calcule à partir du vecteur PT des probabilités du rotamère trans autour des liaisons 0_1, 1_2,...,N-2_N-1. En supposant pour simplifier que les rotamères G et g sont équiprobables, on obtient les vecteurs de probabilités PG¬Pg ¬0.5´1-PT. Partant du tableau CONF des conformations moléculaires, on calcule le vecteur de probabilités PROB de toutes les conformations, par les opérations :

dim¬(3*N-2),N-2

Ptrans¬(CONF='T')´dimrPT

Pgauche ¬0.5´((CONF='G')+CONF='g')´dimr1-PT

PROB¬´/Ptrans+Pgauche

En reprenant l'exemple du tableau 1 avec PT¬0.7 0.5 on obtient ainsi :

Tableau 2

CONF Ptrans Pgauche PROB

TT 0.7 0.5 0.00 0.00 0.3500

GT 0.0 0.5 0.15 0.00 0.0750

gT 0.0 0.5 0.15 0.00 0.0750

TG 0.7 0.0 0.00 0.25 0.1750

GG 0.0 0.0 0.15 0.25 0.0375

gG 0.0 0.0 0.15 0.25 0.0375

Tg 0.7 0.0 0.00 0.25 0.1750

Gg 0.0 0.0 0.15 0.25 0.0375

gg 0.0 0.0 0.15 0.25 0.0375

Les contraintes stériques sont prises en compte en éliminant les conformations où les distances entre atomes non liés sont inférieures à la somme de leur rayon de Van der Waals, ce qui a pour effet de réduire considérablement leur nombre. Ces méthodes mises en oeuvre dans une série de programmes dont CONSTRUC est le noyau commun, sont exposées en détail dans la réf. (6). Voici quelques exemples de leurs applications :

Complexes de coordination paramagnétiques.

Les molécules possédant des groupes polaires entre autre les amines, les alcools ou les phosphates ont la propriété de fixer des ions métalliques dont certains sont paramagnétiques car ils possèdent au moins un spin électronique non apparié. Le moment magnétique correspondant est de trois ordres de grandeur supérieur à ceux des moments nucléaires. Il exerce un champ intense sur les noyaux voisins dont il augmente les vitesses de relaxation et déplace les raies de résonance. Ces propriétés sont mises à profit pour des applications de la RMN au conformations des molécules en solution (7). La figure 3 représente le complexe de coordination qui a servi de modèle pour la mise au point de nos programmes.

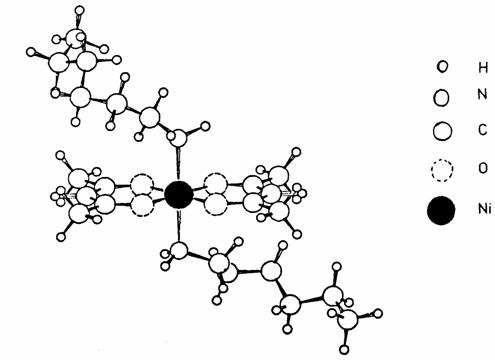
Figure 3. Complexe de l'hexylamine avec l'acétylacétonate de Nickel.

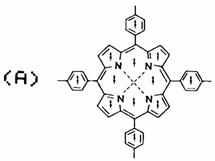
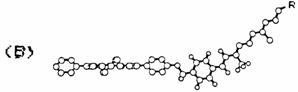
Caroténoporphyrines

Le champ magnétique induit par la circulation des électrons dans un cycle aromatique peut être assimilé à celui provenant d'un dipôle magnétique en son centre et déplace les résonances des noyaux voisins. Cet effet a été utilisé pour déterminer les conformations des caroténoporphyrines possédant une chaîne carotenoïde liée à un macrocycle porphyrine qui comporte 12 dipôles de ce type. Les caroténoporphyrines servent à étudier les transfert d'énergie entre la chlorophylle et le carotène qui interviennent en photosynthèse.

Figure 4. (A) Dipôles magnétiques créés par les courants de cycle de la tétraphényl-porphyrine. (B) Conformation d'une caroténoporphyrine déterminée par RMN du proton (8).

Micelles et cristaux liquides

Au delà d'une concentration critique, les molécules tensioactives forment au contact de l'eau des agrégats sphériques, les micelles (figure 5). En solution concentrée, les micelles peuvent fusionner pour donner des phases cristallines liquides. Ces différents stades impliquent des changements dans les conformation et la dynamique des molécules tensioactives qui tendent à s'orienter perpendiculairement à l'interface de ces agrégats avec l'eau en occupant un volume minimum. La relaxation nucléaire est la méthode la plus spécifique pour étudier ces phénomènes. Nous avons utilisé la relaxation du carbone 13 induite soit par un ion paramagnétique à l'interface eau/agrégat, soit par les protons de la chaîne hydrocarbonée (9).

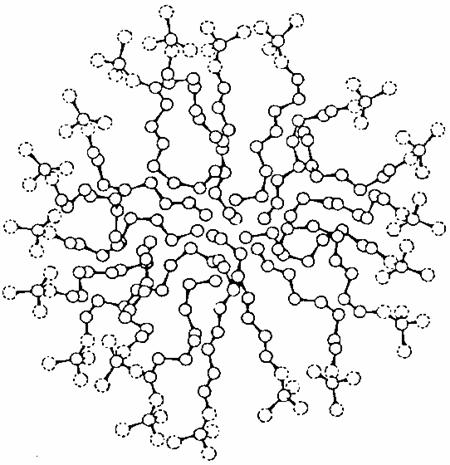
Figure 5. Micelle d'octylphosphate de sodium.

Le programme CONSTRUC a été également utilisé dans une étude récente sur l'intéraction d'échange entre deux spins électroniques localisés à chaque extrémité de la chaîne flexible d'un biradical nitroxyde (10). Le paramètre d'échange moyenné sur toutes les conformations est ajusté de façon à reproduire au mieux le spectre de RPE du biradical.

Ces quelques exemples montrent la diversité des applications de programmes créés au cours d'une dizaine d'année de collaboration avec Gérard Langlet dont certains sont encore utilisés. Je crains que Gérard n’ait pas sauvegardé le système GEOMOL et les programmes qu’il contient pour dessiner les molécules. J’ai par contre conservé le programme CONSTRUC avec ses sous-fonctions, qui sont listés en annexe.

Ma collaboration avec Gérard s'effectuait sous forme de discussions informelles, généralement assez brèves. En plus de son talent d'informaticien, il avait en effet une connaissance approfondie de la physico-chimie qui lui permettait de saisir rapidement tous les aspects d'un problème que je lui exposais. Il m'a par ailleurs aidé à utiliser efficacement APL en me donnant des conseils pour réduire le temps et l'espace nécessaires à l'exécution des programmes. De tous les chercheurs que j'ai rencontré, c'est incontestablement Gérard qui a eu l'influence la plus positive sur mon travail et je lui en suis très reconnaissant.

Références

1 G. Langlet

Journal of Applied Crystallography, 5, 66 (1977).

2 M. Morange, A. Kolb, H. Buc, C. Chachaty et G. Langlet

European Journal of Biochemistry, 74, 99 (1977).

3 C. Chachaty et G. Langlet

FEBS Letters, 68, 181 (1976).

4 C. Chachaty, B. Perly, A. Forchioni et G. Langlet

Biopolymers, 19, 1211 (1980).

5 P.J. Flory,

Statistical Mechanics of Chain Molecules, Interscience, New-York 1969

6 C. Chachaty et G. Langlet

Journal de Chimie Physique, 82, 613 (1985).

7 C. Chachaty, B. Perly et G. Langlet

Journal of Magnetic Resonance, 50, 125 (1982).

8 C. Chachaty, D. Gust, T.A. Moore, G.A. Nemeth, P.A. Liddel et A.L. Moore

Organic Magnetic Resonance, 22, 39 (1984).

9 C. Chachaty et Th. Bredel

Journal of the Chemical Society, Faraday Transactions, 88, 1893 (1992).

10 C. Chachaty, S. Gambarelli et A. Rassat

Magnetic Resonance in Chemistry, 33, S174 (1995).

Programmes de Gérard Langlet pour la géométrie des molécules à chaîne flexible.

Le programme CONSTRUC calcule les coordonnées des atomes pour la forme initiale de la chaîne contenue dans le plan XY de la figure 2 puis, à l’aide de la fonction ROTTI, effectue ce même calcul pour tous les isomères possibles de cette chaîne en effectuant des rotations autour des liaisons successives.

CONSTRUC;S;A;B;C;L;Q;VL;VA;n;ŒIO;chi;D;K

ŒIO„0 ª A„'HCNOSPFc',0½B„'-¸=¬',0½b„'1A23',0½n„'non defini:'

E:…(3>½S„S‡,0½S„½„'CHAINE?')/E

–(0¹L„S¹C„A,B)/'…E,½Œ„''INTERDIT : '',(~L)/S'

S„(S¬' ')/S„,S,[0.5]' -'[(¯1‡L^1²L„S¹A),0]

Z[L/¼½S]„b[B¼(L„S¹B)/Z„S]

Z„((½Z)½ 1 0)š³ 0 1 2 3 4 ²(5,½Z)½Z

–(1¹N„2¬ŒNC Q„ ¯2 0 ‡Z)/'…0,½Œ„n,,'' '',NšQ'

'ATOMES : ',6‡,(((½AT),7)½' '),AT„(S¹A)/S

'NUMEROS : ',6‡ 8 0 •¼½AT

'ANGLES : ', 8 2 •-VA„((½VA)½ ¯1 1)×VA„–,',',Q

–(1¹N„2¬ŒNC Q„ ¯1 ¯2 ‡Z)/'„0,½Œ„n,,'' '',N¬Q'

'LIAISONS : ', 8 2 •VL„–,',',Q

Z„0,[0]+™(K,[0.5]-K„VL×(½VL)½ ¯1 1)×³ 2 1 °.±±-\1,|VA÷180

chi„((D„¯2+1†½Z)½0)°.+ 0 120 ¯120

'Taper 1 pour CHI standard (0 120 ¯120)' ª …('1'=1†,)/EC

ER:'ENTRER ',(•3×D),' VALEURS'

–((3×D)¬×/½chi„Œ)/'…ER,½Œ„''Nb. de valeurs incorrect'''

chi„´(D,3)½chi

EC:Z„(CHI„chi)ROTTI Z,0

'Coordonnées : résultat dans Z. Dimensions : ',½Z

b„½Z ª QFR11„˜0.5+10000×Z

R„CHI ROTTI T;G;H;K;U;D;M;N;Q;CH;L;C;W;ŒIO

ŒIO„0

–(2¬½½CH„-±CHI÷180)/'½R„0½Œ„''CHI : ERREUR'''

–((3>N„1†½T)Ÿ 3 2 Ÿ.¬(¯1†½T),½½T)/'…½R„0½Œ„''T . ERREUR'''

–((¯2+N)¬1†½CHI)/'…R„0½Œ„''CHI doit avoir 2 lignes de moins que T'

G„1†½L„´L÷((+/L×L„(1 0 ‡ ¯1 0 ‡T)- ¯2 0 ‡T)*0.5)°.+3½0

M„((2 0 2 1 ³L°.×L)°.+K[1]½0)×(3 3 ,K„½C)½1-C„2±CH

Q„C,[0] 1 0 1 2 ³(L,-L)°.×S„1±CH

M„M+(3 3 ,½C)½Q[0 3 5 6 0 1 2 4 0 ;;] ª H„2†N-1 ª W„½T

E:R„ŒEX 'R'

T„T-W½T[H[0]-2;] ª R„(H‡T)+.×M[;;0;] ª M„ 0 0 1 0 ‡M

D„½R„ 0 2 1 ³R ª R„((×/2†D),2‡D)½R ª W„½T„((0 3 +H)†T),[0]R

…E—¼2ˆ1†H„H- 1 0 ª R„T

La fonction FTGg construit le tableau de caractères qui donne les rotamères T, G et g autour des liaisons 0_1, 1_2,...,N-2_N-1 où N est le nombre des atomes de la chaîne, correspondant au tableau des coordonnées (voir tableau 1 et figure 2).

FTGg N;ŒIO;K;j;B;D

–(N^.¬ 3 4 5 6 7 8 9)/'…0,½Œ„''NON! SCAL. DE 3 A 9'''

D„1‡½TCH„ 0 1 ½' '

E:TCH„(D† 1 0 •N),[ŒIO„0]TCH ª K„½B„,³(3,½B)½B„TCH[;0]

B„(K½B),[0.5]K½'TGg' ª j„½TCH„ 0 1 ‡TCH

D„½TCH„(K,1‡j)½ 1 0 2 ³(3,j)½TCH

D„1‡½TCH„(0 ¯2 -D)†TCH ª TCH[; 0 1]„B ª B„ŒEX 'B'

…(1<N„N-1)/E ª TCH„((2,D)† 2 1 ½'01'),[0]TCH

La fonction Gg indique les occurences des formes locales Gg ou gG pour éliminer éventuellement les conformations stériquement défavorables qui en contiennent (cf. réf. 5). Cette fonction ne s’applique pas à la liaison 0_1, non plus qu’à la liaison N-2_N-1 si la chaîne se termine par un groupe méthyle (option METH=1).

Gg;B;j;ŒIO;A

–(2¬ŒNC 'TCH')/'…0,½Œ''FAIRE EN PREMIER . FTGg'''

TCH„ 0 1 ‡TCH ª A„'G'= 0 ¯1 ‡TCH ª j„'g'= 0 1 ‡TCH ª A„A^j j„ŒEX 'j'

B„'g'= 0 ¯1 ‡TCH ª j„'G'= 0 1 ‡TCH ª B„B^j ª j„ŒEX 'j'

A„AŸB

A„ 0 1 ‡AŸB ª B„ŒEX 'B' ª –(METH¬1)/'NGg„+/A'

–(METH=1)/'NGg„+/(0 ¯1‡A)' ª A„ŒEX 'A' ª Ng„TCH¹'Gg'

Les fonctions FTGg et Gg sont utilisées pour déterminer le vecteur de probabilités des conformères comme expliqué dans le texte (voir également le tableau 2).