De l'algèbre matricielle au langage

en effleurant chimiquement le code génétique

Par Gérard A. Langlet

 

 

Hypercercles et Equivalents Matriciels

 

 

Soit M une matrice carrée de rang n composée exclusivement de 0 et de 1. Son déterminant, considéré modulo 2, est soit 0 soit 1, nécessairement.  Lorsque ce déterminant vaut 0, il n'existe pas de matrice IM telle que le produit matriciel modulo 2 de IM par M (ou de M par IM) ait pour résultat I la matrice-unité conforme c'est-à-dire de même rang n.

 

Le déterminant d'une telle matrice I vaut toujours 1 , modulo 2 ou non. Si le déterminant modulo 2 de M vaut 1, alors IM existe et son déterminant vaut également 1.

 

Le déterminant classique de la matrice inverse d'une matrice inversible quelconque est toujours l'inverse de celui de la matrice inversée.  Si on divise tous les termes d'une matrice inversible quelconque par le déterminant de cette matrice, on obtient un couple formé par le déterminant d'une part, et une nouvelle matrice dont le déterminant vaut 1, d'autre part.

 

On peut considérer que toute matrice inversible se décompose en un module (son déterminant), et en une matrice normalisée M de module toujours égal à 1. Alors, on peut remplacer le mot module par rayon, et la matrice normalisée inversible par un point situé sur un cercle trigonométrique représenté dans le plan complexe.  Toutes les matrices-unité se situent, pour tout rang n, sur l'axe réel au point habituellement désigné par 1. Le rayon vaut 1 et l'argument (angle au centre en représentation complexe polaire) est nul.

 

Si une matrice inversible M est de rang 2, sa matrice normalisée M (dont le déterminant vaut 1) est une matrice de rotation dans le plan, nécessairement.  Elle s'identifie avec cet angle-argument qui représente, sur le cercle trigonométrique, l'angle à parcourir pour passer de l'angle nul, celui de la matrice­unité, à elle-même.

 

Puisque la transformation, exprimée par la matrice inverse normalisée IM, est une rotation de même angle et de sens opposé, il s'ensuit que cette matrice inverse correspond à un point du cercle trigonométrique situé à la même abscisse, mais avec une ordonnée de signe opposé : on tourne dans l'autre sens : ce point est symétrique du point représentatif de la matrice M par rapport à l'axe réel.  IM est donc le conjugué complexe (unique) de M, et inversement.

 

Lorsque M, matrice normalisée supposée inversible, est de rang supérieur à 2, cette matrice s'identifie à un point d'une sphère hypercomplexe.  Pour le rang 3, cette sphère est une "sphère trigonométrique;" la matrice, inversible, est définie dans une base vectorielle à 3 vecteurs indépendants, orthogonaux entre eux, formant un trièdre euclidien Oxyz direct.  Un des trois axes, par exemple Ox, peut toujours être considéré comme l'axe réel, les deux autres étant des axes virtuels 1 et 2. Le plan passant par le centre de la sphère (point 0, origine O), le point unité ( 1, 1 sur l'axe réél) et par le point représentatif de la matrice sur la sphère, coupe cette dernière en définissant un grand cercle que l'on peut considérer comme un cercle trigonométrique classique : on se trouve ramené au cas précédent.

 

Le parcours à effectuer sur cette section plane, depuis le point 1 (matrice-unité de même rang, ici 3) vers le point représentatif de la matrice M, va correspondre à un angle : M, normalisée, est une matrice de rotation dans l'espace, autour d'un axe passant par l'origine et perpendiculaire à la figure, réductible à une matrice de rotation dans le plan, du même angle, autour de l'origine.  Nécessairement, le point représentatif de la matrice IM inverse unique de M, se trouve dans le même plan de figure, et correspond à une rotation dans le plan du même angle et dans l'autre sens.

 

Le même raisonnement peut être tenu quel que soit le rang de la matrice, avec des hypersphères que l'on va couper par un plan qui aura toujours la même propriété essentielle : celle de contenir aussi le point inverse unique représentatif de la matrice IM inverse de M, en tant que complexe conjugué du point représentatif de M.

Cette propriété est indépendante du rang et de l'algèbre de description qui peut être soit une algèbre hypercomplexe, soit une algèbre entière modulo p (algèbre p-adique); elle est vraie en particulier pour p valant 2, donc en algèbre diadique, celle de l'ensemble Z/2Z qui ne concerne que les deux nombres 0 et 1.

 

Or, il se trouve

 

a) que 0 et 1 sont les deux seuls nombres que sache gérer un ordinateur;

 

b) qu'il est possible d'exprimer tout signal (donc toute mesure) avec 0 et 1 seuls ;

 

c) que 0 et 1 sont les deux SEULS nombres qui, élevés à une puissance p réelle positive quelconque, sont idempotents :0^p vaut 0 et 1^p vaut 1.

 

Cette dernière propriété implique nécessairement qu'il sera possible, par une transformation linéaire, de passer de toute modulation d'un signal, exprimée par 0 et 1, à toute autre modulation de même dimension (nombre de bits).

 

L'algèbre de Z/2Z est la seule algèbre dans laquelle on puisse a priori faire disparaître toute non-linéarité, ce qui est strictement IMPOSSIBLE dans les autres algèbres, à savoir celle(s) que les physiciens utilisent... quotidiennement.

 

Alors, dans cette algèbre de Z/2Z, toute transformation utile, linéaire par essence, va pouvoir s'exprimer, directement dans le langage de l'ordinateur, par des matrices composées de 0 et 1 seulement, c'est pourquoi il devient urgent d'en exposer les propriétés, actuellement ignorées des physiciens.

 

On peut déjà déduire des raisonnements ci-dessus :

 

a)      que des matrices binaires inversibles vont, au fur et à mesure que leur rang va croître, remplir, de manière de plus en plus dense, des hypersphères dont les sections bidimensionnelles passant toujours par le centre seront toojours des cercles trigonométriques vus dans le plan complexe, eux-mêmes remplis de manière de plus en plus dense.

 

b)      que la représentation de nombres complexes et d'angles, donc l'étude, ignorant les formules trigonométriques classiques, va pouvoir se faire avec 0 et 1 seuls, sans que l'on ait besoin de définir pour cela d'autres classes de nombres, comme les nombres négatifs, les nombres rationnels, les nombres irrationnels, les nombres transcendants (e et p) ou encore la constante complexe i (rappelons que -1 ne peut exister modulo 2), la fonction sinus, la fonction cosinus, etc...

On peut en donner un exemple très simple, avec des matrices de rang 2, codables dans un ordinateur en quatre bits seulement, puisqu'elles n'ont que 4 termes.

 

La matrice suivante :

 

|1 1|    a pour carré (produit matriciel par elle-même)

|1 0|

 

|2 1|    qui correspond, modulo 2, à  |0 1|

|1 1|                                 |1 1|

 

         a pour cube (double produit matriciel par elle-même)

 

|3 2|    qui correspond, modulo 2, à  |1 0|

|2 1|                                 |0 1|

 

      a pour bicarré (produit matriciel du carré par lui-même)

 

|5 3|    qui correspond, modulo 2, à  |1 1|

|3 2|                                 |1 0|  

 

Il ressort de ce simple examen, car on pourrait continuer la construction,

 

a)     que chaque puissance matricielle successive de ladite matrice (ici à partir de la troisième puissance, le cube) est la somme, terme à terme, des deux précédentes, (la suite matricielle devenant une suite matricielle de Fibonacci),

 

b) que ces matrices, toutes symétriques, contiennent toujours, dans leurs deux premières lignes ou colonnes, deux nombres entiers successifs de la suite de Fibonacci, alors que les secondes lignes ou colonnes contiennent les deux nombres successifs précédents de la même suite (il s'ensuit que les rapports de deux puissances successives terme à terme vont tendre vers le nombre d'or si on itère l'élévation en  puissance),

 

c)      que la période, lorsque les résultats sont considérés modulo 2, vaut 3, donc  que les trois puissances successives modulo 2 (par exemple les puissances 1, 2 ainsi que 3, la matrice-unité) sont des racines cubiques de l'unité, exactes, strictement équivalentes aux nombres complexes j, j²et 1.

 

On peut d'ailleurs vérifier que la somme des trois matrices

 

|1 1| + |0 1| + |1 0| donc |2 2| vaut bien |0 0| modulo 2

|1 0|   |0 1|              |2 2|           |0 0|

 

comme il convient pour la somme des n racines n^ièmes de l'unité, dans toute algèbre avec laquelle on puisse les défmir. 

 

 

 

 

 

 

 

 

 

 

 

 

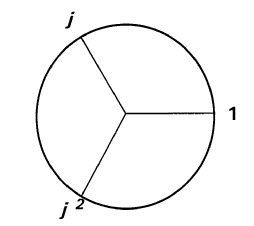
Déjà, on a pu définir, sans aucune erreur et en quatre bits, deux constantes fondamentales de la physique, les opérateurs de rotation ternaire de l'espace métrique tridimensionnel autour de l'axe du temps, dans un sens ou dans l'autre, car le carré de l'une des deux matrices autres que la matrice-unité est aussi,  nécessairement, son inverse matriciel unique, et également, comme on l'a expliqué plus haut, son conjugué complexe.

 

Note. Avec la représentation traditionnelle des nombres complexes basées sur des axes carétsiens (a+bi), il était impossible de définir en toute rigueur j et j² dans un ordinateur, car la partie imaginaire est irrationnelle (±sinus de 2p/3), même en double précision (en consommant néanmoins 128 bits de mémoire ainsi parfaitement gaspillés, alors que quatre suffisent).

 

On peut aisément montrer qu'il existe, pour tout rang de 2 à l'infini, des matrices (appelées génitons) exprimées par 0 et l seulement, et qui aient la même propriété :

 

II suffit pour cela de considérer, pour un rang quelconque, l'ensemble des matrices suivantes (l'exemple choisi, reproduit ci-dessous, à gauche, se rapportant au rang 9), dont chaque colonne, complétée par des 0, contient les coefficients du binôme: la matrice est donc un triangle de Pascal immergé dans une matrice carrée :

 

|  1  1  1  1 1 1 1 1 1|    |0  0  0  0  0   0   0   0   1|

|  8  7  6  5 4 3 2 1 0|    |0  0  0  0  0   0   0   1  ¯8|

| 28 21 15 10 6 3 1 0 0|    |0  0  0  0  0   0   1  ¯7  28|

| 56 35 20 10 4 1 0 0 0|    |0  0  0  0  0   1  ¯6  21 ¯56|

| 70 35 15  5 1 0 0 0 0|    |0  0  0  0  1  ¯5  15 ¯35  70|

| 56 21  6  1 0 0 0 0 0|    |0  0  0  1 ¯4  10 ¯20  35 ¯56|

| 28  7  1  0 0 0 0 0 0|    |0  0  1 ¯3  6 ¯10  15 ¯21  28|

|  8  1  0  0 0 0 0 0 0|    |0  1 ¯2  3 ¯4   5  ¯6   7  ¯8|

|  1  0  0  0 0 0 0 0 0|    |1 ¯1  1 ¯1  1  ¯1   1  ¯1   1|

 

La matrice de droite est l'inverse de celle de gauche. Chaque terme de l'une est symétrique d'un terme égal en valeur absolue dans l'autre, par rapport au point central des deux matrices (ici l souligné au croisement des diagonales, comme

pour tout rang impair, mais qui tomberait au centre de quatre termes pour tout rang pair), cette propriété va se conserver module p, avec p entier, en particulier si p vaut 2.  Et, dans ce dernier cas, la restriction sur la valeur absolue disparaît, puisque l'algèbre de Z/2Z est non signée.

 

Dans le cas à gauche ci-dessous, la matrice est le retournement vertical dans le plan, de la matrice de gauche ci-dessus; par symétrie, le même raisonnement s'applique également au retournement horizontal, matrice transposée de la matrice ci-dessous à gauche; la matrice de droite est encore l'inverse matriciel de cette dernière; cette fois, les termes ne subissent plus de symétrie par rapport au centre; en algèbre module p avec p valant 2, il existera donc un couple de matrices auto-inverses, pour tout rang, de 2 à l’infini.

 

| 1 1 1 1 1  1  1  1  1|    |1 ¯1  1 ¯1  1  ¯1   1  ¯1   1|

| 0 1 2 3 4  5  6  7  8|    |0  1 ¯2  3 ¯4   5  ¯6   7  ¯8|

| 0 0 1 3 6 10 15 21 28|    |0  0  1 ¯3  6 ¯10  15 ¯21  28|

| 0 0 0 1 4 10 20 35 56|    |0  0  0  1 ¯4  10 ¯20  35 ¯56|

| 0 0 0 0 1  5 15 35 70|    |0  0  0  0  1  ¯5  15 ¯35  70|

| 0 0 0 0 0  1  6 21 56|    |0  0  0  0  0   1  ¯6  21 ¯56|

| 0 0 0 0 0  0  1  7 28|    |0  0  0  0  0   0   1  ¯7  28|

| 0 0 0 0 0  0  0  1  8|    |0  0  0  0  0   0   0   1  ¯8|

| 0 0 0 0 0  0  0  0  1|    |0  0  0  0  0   0   0   0   1|

 

On peut démontrer ces propriétés par celles des coefficients du binôme et par les formules des combinaisons de N objets P à P. Mais la démontration matricielle, plus générale, permet de s'affranchir de l'écriture d'équations : Dans le développement de y en puissances successives, si on remplace y par x+l, la transformation inverse consiste à remplacer x par y-1; alors les coefficients, termes des matrices inverses l'une de l'autre, sont bien les mêmes partout au mêmes endroits, au signe près, et strictement identiques modulo 2, lorsqu'on ne retient que la parité (reste, toujours 0 ou 1, de la division entière par 2).

 

En une seule courte démonstration, on prouve ainsi que tous les triangles de Sierpinski, fractals célèbres, parités des triangles de Pascal, disposés ainsi en matrices carrées non triviales, sont, pour tout rang, selon leur disposition, soit auto-inverses, soit inverses de leur carré matriciel, donc constituent, dans ce dernier cas des représentation rigoureuses des racines cubiques complexes de l'unité, opérateurs de rotation ternaire de notre "espace-temps" traditionnel.

 

On peut aussi démontrer que tous les carrés matriciels des matrices de Pascal, dans lesquelles les coefficients du binôme sont disposés verticalement, ont pour résultat des matrices dont tous les termes ont la même parité que celle de leur inverse matriciel.  Modulo 2, les carrés et les inverses sont identiques.  Le carré de la première matrice de rang 9 à disposition verticale présentée plus haut; est reproduit ci-dessous à gauche, sa parité étant reproduite à droite :

 

| 256  128  64  32  16   8   4   2   1| |0 0 0 0 0 0 0 0 1|

|1024  576 320 176  96  52  28  15   8| |0 0 0 0 0 0 0 1 0|

|1792 1120 688 416 248 146  85  49  28| |0 0 0 0 0 0 1 1 0|

|1792 1232 832 552 360 231 146  91  56| |0 0 0 0 0 1 0 1 0|

|1120  840 620 450 321 225 155 105  70| |0 0 0 0 1 1 1 1 0|

| 448  364 292 231 180 138 104  77  56| |0 0 0 1 0 0 0 1 0|

| 112   98  85  73  62  52  43  35  28| |0 0 1 1 0 0 1 1 0|

|  16   15  14  13  12  11  10   9   8| |0 1 0 1 0 1 0 1 0|

|   1    1   1   1   1   1   1   1   1| |1 1 1 1 1 1 1 1 1|

 

 

Matrices Pentagonales

 

La figure suivante n'est qu'un exemple; on peut la construire avec des polygones réguliers à un nombre quelconque de côtés.

 

Soit une matrice normalisée M, ne contenant que 0 ou 1, telle que son élévation à la puissance 5 ait pour résultat une matrice unité I. (voir l'exemple proposé deux pages plus loin).

 

On peut concevoir qu'elle représente un sommet d'un pentagone régulier dont les autres points-sommets sur un cercle trigonométrique sont les puissances successives M², M³, M⁴ et M⁵ de ladite matrice

 

 

 

 

 

 

 

 

 

 

 

 

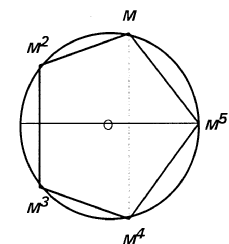
M⁵ est aussi I. Alors, M est inverse de M⁴ tandis que M² est inverse de M³, sur ce cercle trigonométrique, et réciproquement. Les nombres complexes correspondants (en fait des nombres hypercomplexes), sont conjugués deux à deux par rapport à l'axe réél. 

Il en serait de même pour toute matrice normalisée, quelle que soit la puissance de cette matrice qui s'identifie à I l'unité.

Or, pour un rang fini quelconque n, le nombre de combinaisons de matrices différentes possibles (carrées) ne contenant que 0 ou 1 est 2ⁿ² donc fini. Une proportion minoritaire d'entre elles a un déterminant non nul. En itérant le produit matriciel modulo 2, d'une matrice normalisée, par elle-même, on obtient nécessairement d'autres matrices dont le déterminant vaut toujours 1, donc dont les arguments sont toujours espacés d'un même angle sur le même cercle trigonométrique qui les porte en tant que points. 

Supposons qu'on ne parvienne jamais sur le point I (ou 1) l'unité. Il faudrait alors que les puissances successives, ou bien forment une suite infinie de matrices différentes (non congruentes) ce qui est impossible pour un rang fini, ou bien que les sommets du polygone régulier sautent la valeur 1 : le polygone serait déphasé.  Il est obligatoire que l'on retombe, à un moment quelconque, sur un sommet déjà connu, quel que soit le parcours, et ce, dans les deux sens, c'est-à-dire si l'on itère la multiplication matricielle sur la matrice inverse, unique, et conjuguée de M. Par symétrie, un de ces sommets déjà connus doit se situer sur l'axe de symétrie du système, l'axe réél. On ne peut, pour un nombre de sommets impair (donc un polygone dont on réunit les points par argument croissant (modulo 2p) que tomber sur le point réél appelé 1 ou I. Pour un nombre de sommets pair, on passera aussi par une matrice non triviale, nécessairement auto-inverse, représentant une pseudo constante  -1 située sur l'axe réél à l'opposé de 1.

 

Mais il résulte de ce raisonnement que toute matrice normalisée M admet une puissance k (entier positif) identique à une matrice-unité, et, qu'en conséquence, la puissance k-1 de M est aussi la matrice inverse de M ET son conjugué hypercomplexe. Si k est pair, il existe en outre une matrice puissance (k/2)^ièmede M, nécessairement auto-inverse modulo 2, et qui n'existe pas si k est impair.

 

On pourra, en résumé, assurer toute transformation sur n’importe quel type de problème, de manière linéaire, en mettant à profit l'algorithmique simple et précise qui va résulter de ces propriétés des matrices dans Z/2Z, directement dans la mémoire des ordinateurs, et ce avec toute la précision nécessaire, sans utiliser d'autres applications autres que celles qui sont nécessaires pour programmer des produits matriciels sur des bits.

 

Or, le produit matriciel est une loi de composition interne sur l'addition et la multiplication, opérations qui se réduisent, en algèbre logique isomorphe de l'algèbre entière modulo 2, à l'équivalent logique de ces opérations considérées modulo 2.

 

Comme la disjonction - le Ou Exclusif logique - (notée Å en mathématiques, mais simplement ¹ dans la norme internationale IS08485) correspond à l'addition modulo 2 et que la conjonction ET logique (notée Ù) correspond à la multiplication modulo 2, la loi de composition interne ¹.Ù peut désormais symboliser le produit matriciel (et aussi le produit scalaire) dans tous les cas ; mais, pour simplifier, on peut utiliser le symbole "." (point gras), dans la notation, comme on le fait couramment d'ailleurs en calcul matriciel classique.

 

Annexe : Exemple de matrices normalisées racines 5^e de l'unité (il n'en existe pas pour un rang inférieur à 4):

 

Puissance:      1         2             3         4         5

 

            |1 1 1 0| |0 0 1 1|     |1 1 0 0| |1 0 0 1| |1 0 0 0|

            |0 1 1 1| |1 0 1 1|     |0 0 1 0| |1 0 1 0| |0 1 0 0|

            |1 0 1 0| |0 1 0 0|     |0 1 1 1| |1 0 1 1| |0 0 1 0|

            |0 1 1 0| |1 1 0 1|     |1 1 1 1| |0 1 0 1| |0 0 0 1|

 

Règle (propriétés quantiques des matrices binaires ou de Z/2Z)

 

- Une matrice normalisée de rang n sera au maximum racine 2ⁿ-1 de l'unité.

 

C'est ainsi qu'une matrice M de rang 2 peut être soit racine carrée soit racine cubique de l'unité, et que des éléments de symétrie supérieurs à des groupes d'ordre 3 ne peuvent intervenir pour des états de couples interagissant l'un sur l'autre.

 

Exemples de tels couples de bits, parités ou spins, en général décrits par d'autres notations, selon les habitudes de différentes disciplines scientifiques :

 

|XX| parités sexuelles, |↑↑‌ spins   (état triplet),

|XY|           |↑↓‌            (état singulet);

 

 

                 |AA|  |BB|   groupes sanguins,

                 |AO|  |BO| (et bien d'autres facteurs du système immunitaire)

 

Ces matrices de deux états sont isomorphes de la matrice normalisée racine cubique de 1'unité j, le 2-géniton G

 

|1 1|

|1 0|

 

et décrivent, effectivement, les états possibles pour les systèmes observables à deux parités différenciées.

 

Il résulte également de ce qui précède, qu'une évolution dynamique de systèmes peut se décrire par des multiples d'angles (nécessairement considérés modulo 2p), donc par de simples sommes angulaires successives; si les mesures que l'on effectue (et c'est ce qui est en général le cas), ne permettent pas de connaître les variations sur l'ensemble des axes orthogonaux relatifs aux multiples parités des systèmes, on risque d'aboutir à des formules qui seront seulement approximatives.

 

Un exemple notoire de cette incomplétude se retrouve par exemple dans les équations logistiques, mais aussi dans toutes les mesures spectrales : on relève des intensités mais non des amplitudes; on n'a pas accès à la phase du système, ce qui revient, par exemple, à essayer de comprendre l'évolution d'une population (qu'il s'agisse d'électrons, d’individus, d'espèces chimiques, biologiques ou monétaires), avec pour seul paramètre le comptage de cette population.

 

Ainsi, dans le plan complexe, ne disposerait-on que d'une information relative à un seul axe (réel ou imaginaire, le choix est indifférent, car cette notation n'est qu'une affaire de convention).

 

Une application telle que a¬2a va impliquer, si elle est itérée, un angle qui double chaque fois, ce qui correspond à l'élévation au carré d'une variable complexe Z. On aurait alors, en la décrivant ainsi, une application itérée de formule Z¬Z²+c (c étant une constante a priori complexe, mais ici nulle, introduite seulement pour bien montrer la parenté qui existe avec les formules de Fatou et Julia, popularisées par Mandelbrot).

 

La connaissance d'un paramètre mesuré sur l'un des axes de projection, non plus comme une amplitude, mais comme une intensité, donc comme un carré, peut avoir tendance à faire prendre pour variable x le carré d'une seule des deux projections, par exemple sin²a si a est la vraie variable (cachée).  Alors, si l'angle prend une valeur double entre deux mesures, ce que l'on va observer, le nouvel x, correspondra (sans que l'on s'en doute) à sin²2a, formule qui, grâce à la trigonométrie classique devient : (2 sina cosa)² donc 4 sin²a cos²a ou encore 4sin²a(1-sin²a) c'est-à-dire finalement x¬4 x (1- x). (On obtiendrait un résultat analogue en considérant l'autre axe, avec un déphasage de p/2, mais la démonstration serait légèrement moins courte).  Voici peut-être pourquoi cette équation logistique, qualifiée de non linéaire (elle est effectivement non linéaire en x) car elle s'exprime à l'aide d'un paramètre qui est insuffisamment analysé, a pu faire illusion sinon fureur, dans de très nombreuses disciplines depuis environ 130 ans : proposée par Verhulst au siècle dernier, elle a été reprise, en physique comme en médecine, en écologie aussi bien qu'en analyse financière, et fait encore, de nos jours, des gorges chaudes dans la théorie du chaos; on cherche encore aussi à comprendre et à formuler ce chaos à l'aide d'équations à variation continue, alors que toutes les mesures que l'on puisse effectuer physiquement, ainsi que nos perceptions, sont toujours des échantillonnages discrets des phénomènes!  L'algèbre des parités va permettre, espérons-le, de mieux comprendre les systèmes complexes comme des assemblages de tout OU (Exclusif) rien, et de simplifier drastiquement les calculs, en rendant intégrable, puisque linéaire et précis, ce qui ne l'était pas, autrement.

 

Toutefois, ce type d'équations aura été utile pour montrer :

 

a) qu'il existe une unité dans le comportement de TOUS les systèmes dynamiques donc évolutifs,

 

b)  qu'il existe des états stationnaires (en écologie, comme en chimie industrielle, on parle de régulation).

 

Ainsi, dans l'équation précédente, x est fixe si ce paramètre vaut 3/4.  Mais alors, quel est le sens physique d'une telle constante ?

 

Non seulement on retrouve cette constante, ou son double 3/2 ou son inverse 4/3, sans trop bien la comprendre, dans nombre de formules dans lesquelles intervient ce que l'on appelle la "dimension fractale" (par exemple dans l'absorption ou la transmission de la lumière par les nuages), mais elle est connue... depuis 25 siècles!  On la doit en effet à Pythagore de Samos, qui ignorait, et pour cause, les "fonctions sinusoïdales" et les fréquences, mais découvrit, en pesant des masses (exactement des marteaux de forgerons), ce rapport essentiel pour nos perceptions sonores : 4/3 est le rapport fondamental de l'intervalle de quarte (diatessaron) et 3/2 celui de l'intervalle de quinte (diapente) en musique, donc en acoustique - le doublement étant le rapport de la gamme complète.  Convaincu que les nombres devaient tout expliquer, il déduisit - malheureusement - d'autres rapports fractionnaires d'entiers pour les autres intervalles de la gamme, alors que la seule itération de ce rapport 4/3 dans un sens, ou 3/4 dans l'autre, permet de reconstituer toutes les notes de la gamme chromatique naturelle.

 

Il suffit de s'apercevoir que 3/4 est le carré de Ö3/2 ou, mieux, le produit de iÖ3/2 par -iÖ3/2 c'est-à-dire d'une valeur imaginaire y par son conjugué complexe y*.  Ce produit yy*, fondamental en mécanique quantique, correspond alors directement au produit du sinus de j par celui de j² , preuve, s'il en fallait encore une, que ces deux constantes exprimées maintenant en matrices de parités opposées 0 et 1, gèrent effectivement les transformations de ce que l'on appelle en dynamique l'état stationnaire. Et Fibonacci ne pouvait pas savoir non plus, à la fin du XIIe siècle, lorsqu'il découvrit sa fameuse suite en étudiant la reproduction des lapins, que la seule matrice des micro-gènes sexuels, découverte bien plus tard, codant aussi bien les "êtres vivants", à reproduction sexuée, que les états des électrons et ceux des "magnétons", et reconnue aussi ­indépendamment - par les spécialistes de la phylotaxie (la croissance des plantes), était aussi l'opérateur de transformation, racine cubique de l'unité, de notre espace lui-même.  En cherchant bien, on s'aperçoit maintenant que cette matrice se retrouve partout, et, en particulier, quand il s'agit de coder de l'information essentielle (comme un patrimoine génétique), ainsi que la transmission optimale de cette information.

 

Par exemple, Louis Braille, non-voyant et non mathématicien, âgé seulement de 16 ans, inventa et perfectionna, à partir de 1825, un code d'une efficacité époustouflante, utilisé actuellement sur toute l'étendue de la planète, basé sur les matrices binaires, alors que le binaire fut "réinventé" par George Boole près de 40 ans plus tard : le binaire était connu des Chinois ("Yi^King" ou "Izin", le "Livre des Mutations") depuis des miIlénaires, et fut étudié par Leibniz à la fin du XVII^e siècle, puis réoublié; il fut popularisé, surtout grâce à Claude Shannon, seulement vers la fin des années 1920, et utilisé, pour l'informatique, encore bien plus tard.

 

Une autre découverte, encore plus récente (Crick & Watson, 1954) fut celle de la structure en double hélice de l'ADN (acide désoxyribonucléique) qui code notre patrimoine génétique entier (le génotype), dont notre aspect physique (phénotype) et notre cerveau, donc notre comportement et notre "intelligence".  Tout notre acquis se trouve rassemblé en de longs assemblages moléculaires, les chromosomes, qui, déroulés et mis bout à bout, constitueraient un fil d'Ariane invisible, long d'environ 150 cm.  Un alphabet de 4 lettres - ou, plus exactement de deux fois deux lettres qui se retournent (un peu comme les consonnes respectivement labiale sourde et dentale sonore "b" et "d" ou les consonnes respectivement gutturale sourde "q" et labiale sonore "p"; ces lettres sont les 4 retournements possibles, dans le carré, de la même forme, respectant les compositions de "symétries-miroirs" fondamentales aussi bien dans le graphème que dans la description verbale de leur valeur phonétique - voir l'Annexe).

 

Les quatre lettres du code génétique sont, elles, traditionnellement, les initiales des noms de composés chimiques (bases puriques et pyrimidiques) qui se lient entre elles deux à deux.  Ainsi la base T (thymine) se lie à la base A (adénine) pour former la paire AT (appelée simplement A); la même paire, alors retournée, devient TA (appelée simplement T).  De même, la base G (Guanine) se lie à la base C (Cytosine), pour former la paire GC (appelée simplement G), cette paire, retournée à son tour, devient CG (appelée simplement C).  Un assemblage de 3 de ces lettres (ici en gras), parmi 4, tel que GAG ou ATC est un "mot vivant" ; ces mots sont capables de coder, accolés dans des phrases, toutes les protéines qui nous composent.  D'abord, on remarquera ce rapport 3 sur 4, toujours le même.  Mais on peut aller beaucoup plus loin, c'est-à-dire rechercher exactement où se trouve, chimiquement, le code de ces molécules, et sous quelle forme :

 

En examinant de près les formules développées de ces assemblages simples de type Meccano, boîte N° 1, un chimiste remarquera, dans la paire AT un couple et dans la paire GC un triplet de liaisons faibles, faciles à assembler ou à désassembler (comme du Velcro) appelées des liaisons-hydrogène.  Les assemblages des atomes qui portent ces liaisons sont de deux types seulement et ressemblent, comme par hasard, à la fois aux assemblages de parités que Braille utilisa pour coder efficacement sa langue maternelle, et... aux matrices dont il a été question plus haut.

 

Sans entrer ici dans des détails chimiques, on peut penser que Dame Nature utilisa, pour coder le patrimoine génétique du vivant, des éléments chimiques qui se trouvaient, à la surface de notre planète, en quantité non négligeable, à savoir l'azote (N pour "nitrogène") et l'oxygène (O) en priorité.  L'hydrogène H ne manquait pas non plus dans l'eau H₂0 alias aqua simplex.

 

Dans la paire AT et la paire TA (AT retournée), on va trouver l'assemblage schématique de gauche, alors que l'on va trouver l'assemblage de droite dans la paire GC et la paire CG (GC retournée) :

 

  |O N|            |N O|

  |N N|    et     |N N|       |N N|     et    |N N|

  |N O|            |O N|       |N O|             |O N|

 

N N signifie qu'il existe une liaison hydrogène (non figurée ici) entre deux atomes semblables d'azote, et N O signifie qu'il existe une liaison hydrogène entre deux atomes, dissemblables, d'azote et d'oxygène.

 

Avec la notation 1 pour N (majoritaire dans l'atmosphère) et 0 pour O (minoritaire), la configuration de gauche présente une analogie totale avec la matrice sexuelle     |X X|  dans laquelle X est codé 1 et Y codé 0 (le chromosome

             |X Y|  Y est d'ailleurs plus petit que le chromosome X).

 

Une des deux matrices carrées est racine cubique de l'unité et son retournement est racine carrée (modulo 2 comme on l'a vu); 3 sur 4 des positions possibles sont remplies de 1, de N ou de X.

 

Les matrices de droite, comme celles de Braille à partir de la lettre "k", ont 3 lignes et 2 colonnes.  Transcrites en notation 0 1 et immergées dans une matrice carrée (rendue inversible modulo 2) qui a alors le rang 3, elles présentent une symétrie plus complexe (notamment heptagonale) modulo 2.

 

Il reste encore à réfléchir beaucoup sur ces codages qui sont optimaux - ils codent, avec seulement deux fois deux lettres, tout le "vivant" - mais sont loins d'avoir livré leurs secrets; on peut toutefois penser que cette avalanche d'analogies, toutes explicables par des symétries cachées, révélées seulement en algèbre modulo 2, recouvre une unité entre la physique et la biologie bien plus forte qu'on ne l'avait entrevue jusqu'ici ; on pourrait certainement renforcer l'exploration de celle-ci en augmentant le caractère transdisciplinaire de la recherche, et en orientant davantage les capacités de cette recherche, nationale et internationale, vers une étude plus poussée de la nature profonde de l'entité mystérieuse que l'on appelle Information et qu'en réalité on connaît très mal.

 

Annexe Universalité de la Symétrie (application langagière)

 

Dans le langage humain, les symétries surgissent de partout dès que l'on commence à les traquer.  Dans la page précédente, on voit que la forme des symboles comme celle des lettres de notre alphabet, n'est pas quelconque.  Si les minuscules "b" "d" "p" "q" respectent dans leur forme une symétrie d'ordre 4, ce n’est certainement pas par hasard.  "b" est verticalement symétrique de "d", alors que les deux consonnes sont sonores (ou voisées), mais l'une est labiale et l'autre est dentale.  "b" est horizontalement symétrique de "p" alors que les deux consonnes sont labiales mais l'une est sonore et l'autre sourde.  "b" est centro­symétrique de "q" (l'élément de symétrie est un centre) alors que l'une est labiale sonore et l'autre gutturale sourde.  On peut en donner bien d'autres exemples avec les majuscules, les chiffres romains, d'autres alphabets et aussi avec des idéogrammes d'origine diverse.

 

La sémantique et la phonétique sont intimement liées par la symétrie également.  Pour s'en apercevoir, il convient de faire abstraction de l'écriture, surtout dans notre langue dont l'orthographe constitue un parangon d'hyper-complexité.  L'homme parle depuis toujours, mais écrit, et surtout, lit couramment depuis peu. (merci, Jules Ferry).  Des règles aisées à trouver grace à l'établissement de liens forts entre l'algèbre binaire matricielle (logique et modulo2), et les groupes cycliques (discipline actuellement enseignée nulle part ... ) ont récemment permis d'avancer l'hypothèse - (Congrès Int. sur le Chaos et la Complexité, Blois, juin 1993), que les mots et les concepts étaient marqués par les organes - les voies ­qui les émettaient ou les percevaient; la différenciation (comme la reconnaissance) s'effectuerait alors par symétrie, soit préférentiellement sur les voyelles et diphtongues pour les langues où ces dernières jouent un rôle majoritaire - cas de la plupart des langues occidentales vocaliques (indo­européennes) ou agglutinantes (finno-ougriennes), soit sur les consonnes dans le cas contraire (comme dans les langues sémitiques).

 

Quelques exemples, compréhensibles par tout le monde, suffisent à le montrer heureusement, la langue française, comme la langue anglaise qu'elle contamina fortement autrefois, regorgent de mots d'origine diverse, par exemple latine ou grecque.

 

Prenons un mot anglais comme "voice", du français "voix", (du latin "vox, vocis").

 

Décomposons-le délicatement en monèmes (consonnes ou voyelles "atomiques"); nous obtenons quelque chose comme : "V oo ee z".

 

(A noter que les sons "o" et "ou"- "oo" en anglais - dérivent de la meme origine, ils ne sont d'ailleurs pas différenciés du tout dans les langues sémitiques).

 

Permutons les voyelles, ce qui donne : "V ee oo z".  En prononçant cela, on perçoit le mot "Views".  Le premier signifie "ce qui est entendu", le second "ce qui est vu".

 

Un phénomène analogue existe d'ailleurs, toujours en anglais, entre des mots comme : "N ee oo z" ce qui est appris (et espéré bon) et la permutation "N oo ee z" qui perturbe le précédent et est mauvais (le couple "News"/"Noise".  "News" est d'ailleurs aussi bien "ce qui est entendu" que "ce qui est vu et lu").  On peut ajouter que des omissions vocaliques comme "N - oo Z" ou "N ee - z" correspondent à des mots indiquant respectivement ce avec quoi on perçoit ­autrement - à la fois ce qui est bon ou mauvais ("Nose") et ce avec quoi on marche ("Knees").  D'ailleurs, en français la signification est inversée par rapport à la phonétique : "Nez" et "{ge}Noux".

 

La langue française exhibe des homonymies indiquant que le mot se trouve déjà sur l'axe de symétrie vocalique, alors que langue anglaise, avec peu de voyelles pures, permet d'étudier une différenciation qui n'existe plus chez nous phonétiquement, mais subsiste dans l'orthographe... heureusement, parfois.  Ainsi le mot "V wa" ne possède plus deux monèmes vocaliques mais un seul, sur lequel la permutation est évidenunent nilpotente (n'a aucun effet), on ne peut pas non plus omettre une voyelle ou une émission vocalique... qui n'existe pas. Ce qui est entendu est alors "Voix", alors que les flexions "Vois" ou "Voit" se rapportent à ce qui est vu, tout à fait indépendamment de la "Voie" de pénétration.

 

Passons au grec, avec les racines de, justement, ce qui est entendu, "jwnh", "Phônê", la "Voix" - sans laquelle la phonétique n'existerait pas - et de ce qui est vu, ou, plus exactement de ce qui a été vu, observé : "jainomenon" le "phénomène"; le suffixe "me" ("me") indique le passé et "ménos" (neutre "ménon") est le suffixe du participe passé; la diphtongue "ai" ne se prononçait pas "aïe" comme on l'enseigne chez nous en cours de grec classique, mais entre "é" et "ê", comme d'ailleurs, de nos jours en grec moderne.  Bien que les racines latines et grecques "phoné" et "phéno" soient totalement différentes, on est bien obligé de constater que la permutation vocalique agit strictement de la même manière.

 

Avec d'autres racines latines, présentes dans des mots passés en français aussi bien que dans le vocabulaire international, on va retrouver la même loi : Prenons les mots "Audio", relatif à ce qui est entendu, et "Video", relatif à ce qui est vu (respectivement, en latin, "j'entends" et "je vois"). Autrefois, le U, prononcé "ou" et le V n'étaient pas différenciés (voir les incriptions romaines); "v" était une semi-consonne très voisine du "w" anglais.  "W" et "oo" sont le même monème.  "W oo d ee o" et "W ee d e o", prononcés par des Anglais, sont assez proches de la prononciation latine originale; la règle est certes moins nette, mais on la débusque néanmoins encore une fois. De même, en latin, "W ee z oo s", "visus", le "visage", est ce qui est vu, tandis que "W oo z ee s" aurait été compris comme le génitif "vocis" de "vox", "voix".

 

Si l'on prononce "î" "eu", un Anglais entendra "ear", "oreille" et un Français "yeux", alors que si on prononce "eu" "î", un Français percevra "oeil" et un Anglais peut-être "eye" (plutôt prononcé "a" "î"). Mais l'identification phonétique de "eye" au pronom personnel "1", toujours écrit en majuscule, n'est pas non plus un hasard. L'organe permet au "Je" de percevoir l'environnement en écho, comme, en grec, justement, 1"'écho", "en grec "Ecw" reflète 1"'Egw" "Ego", (également en latin, "je" ou "moi"); en grec, les deux consonnes c chi et g gamma sont aspirées, respectivement durement et doucement (comme en allemand "ch" est dur après "a" "o" "u" et doux autrement); mais "Ecw" exprime aussi la possession en signifiant aussi "j'ai" prononcé "jè" en français avec une voyelle sonore alors qu'elle est sourde dans "je". Ce jeu du je est-il un jeu de Lego? Car, même avec un mélange de racines germaniques, grecques et latines ou américano-argotiques, les permutations font la loi (comparer "talk" "t o 1 k" et "glotte" "g 1 o t", "OK" et "KO", qui, bien entendu, s'entend conune "chaos" !).

 

On pourrait objecter que latin, grec, anglais et français sont des langues cousines; alors passons à 1’inversion consonantique de l'arabe, langue dans laquelle les voyelles sont des parents pauvres, apparaissant comme secondaires, pour l'euphonie; en arabe, comme dans d'autres langues sémitiques, les racines essentielles se composent de trois consonnes, dont les flexions vocaliques viennent différencier le sens. (En chinois, les noms propres ont trois syllabes ... )

 

"Ktb" signifie "ce qui est vu", exemple, avec des voyelles : "kitab" . "le livre", l'écrit.  La plupart des Occidentaux connaissent un autre dérivé célèbre de cette racine : alors qu'en grec, "mè" est - entre autres - un suffixe indiquant le passé, comme on vient de le voir avec "phénomène", et qui s'ajoute à droite de la racine, "mè" indique également le passé en arabe, mais, (par symétrie ou contradiction ­car "mê", en grec comme en français "mais", indique encore la contradiction!), "mè" est un préfixe qui se met alors devant : on obtient ainsi : "mèktb", prononcé automatiquement "mèktoub", "ce qui a été écrit, donc lu", alias le fameux "destin incontournable"

 

Alors, si vous voulez vous faire comprendre en Orient, essayez à tout hasard "Bitikallim ingilissi ?" - en anglais "Do you speak English?" Une fois ôtée "allim" la désinence verbale, on s'aperçoit que le radical "btk" relatif à la parole, donc à "ce qui est entendu", présente, comme on aurait pu s'en douter, une nette symétrie par rapport à "ktb" "ce qui est vu", puisqu'il s'agit d'un retournement complet du radical, lequel est aussi triplement consonantique... que les mots du code génétique lui-même.

 

En outre, la langue arabe doit adorer la symétrie numérique, puisque les adjectifs numéraux se mettent au féminin pour s'accorder avec un substantif masculin... et réciproquement.

 

L'opposition vu/entendu se retrouve aussi en vietnamien, et il serait intéressant d'explorer les langues africaines, indiennes et polynésiennes, pourquoi pas ?

 

En réfléchissant bien (car les exemples abondent), il est normal que des individus provenant d'une même origine, tous codés à l'aide du même alphabet génétique, répercutent, à leur insu, dans leur langage naturel, avec les symétries duquel ils jouent parfois (cf. les contrepèteries), comme dans celui qu'ils "inventent" - qu'il s'agisse du braille, du morse ou du verlan - des lois de symétrie binaire qui, manifestement, gèrent dans tous ses aspects un "système général".

 

L'étude de ce dernier, appelé aussi Univers (et pas seulement au sens astronomique du terme), a été abusivement partitionnée, au XX^e siècle surtout, en "sciences dures" et en "sciences molles", pour le plus grand bienfait de l'incompréhension qui semble résulter actuellement de cette dichotomie arbitraire, infiniment regrettable quand on désire comprendre, en tentant de recoller les pièces du puzzle, par un regard orienté tous azimuts.

 

¬\