EXPéRIMENTATION MATHéMATIQUE EN « J »

par Robert  Coquidé

Algorithme : prenons un entier A₀ > 1. S’il est pair, calculons A₁=A₀/2 sinon A₁=(1+3A₀)/2. Puis, calculons A₂ de la même façon à partir de A₁. Et ainsi de suite ... jusqu’à ce que l’on trouve A_n=1.

Conjecture : Pour tout entier A₀ > 1, on obtiendra A_n=1 en un nombre n fini d’itérations.

Cette propriété n’a, semble-t-il, jamais été étayée par une démonstration ni démentie par quelque judicieux contre-exemple.  

Dans ce qui suit, f est un verbe qui calcule A_k+1 à partir de A_k, et g un verbe récursif, utilisant f, qui calcule la suite des nombres obtenus jusqu’à 1.

  f =.-:`(-: @ >:@(3&*))@.(2&|)

 g =.3:'if.2<{:,y.do.g y.,f{:,y.else.y.,1 end.'

 E =.1!:2&2     NB. Verbe monadique qui affiche et retourne son argument.

Utilisation de "plot" (verbe inclus dans la zone plot.js) qui trace un graphique.

Le verbe "suite" ci-dessous calcule cette suite de nombres, trace une courbe représentative, et retourne le nombre d'itérations et le maximum atteint:

suite   =.3:0

(#,>./)E r[plot r=.g y.)

Ex 1:

  suite 7 

 7 11 17 26 13 20 10 5 8 4 2 1  NB. suite d'entiers terminée par 1

12  26   NB. 12 nombres dans cette suite,  nombre maxi de la suite: 26

Chaque "sommet" est précédé par une sous-suite d'entiers impairs et suivi par une sous-suite d'entiers pairs.

Chaque "creux" est précédé par une sous-suite d'entiers pairs et suivi par une sous-suite d'entiers impairs.

Certaines de ces suites comportent un grand nombre de "sommets" et de "creux". Chaque changement de signe de la pente traduit un changement de parité dans la suite de nombres.

Ex2 :

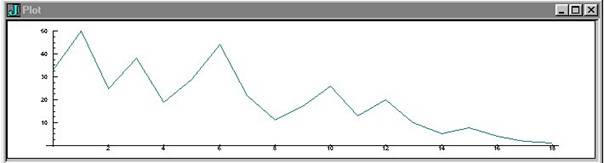
 suite  33

33 50 25 38 19 29 44 22 11 17 26 13 20 10 5 8 4 2 1 50

 En partant d'un nombre de la forme 2^p il n'y a aucun "sommet" et la suite est décroissante jusqu'à la valeur 1.

Ex3 :

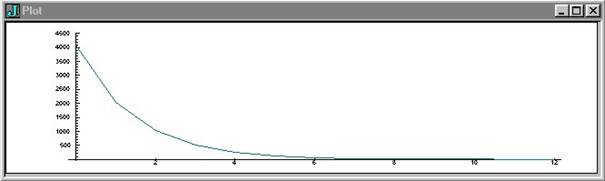
suite  4096

4096 2048 1024 512 256 128 64 32 16 8 4 2 1 13  4096

Un graphique permet d'illustrer la propriété étudiée. Il ne constitue pas une démonstration mais peut, tout au plus, stimuler l'imagination de qui tente d'en établir une. Les personnes pratiquant les mathématiques savent que si le contenu d'une démonstration ne repose que sur "la" logique, le choix de la méthode utilisée fait appel à ce que l'on peut nommer habituellement le flair (ou "pifomètre"), souvent l'imagination, parfois l'intuition, plus rarement le talent…, et, très exceptionnellement, le génie! 

              Ici, certaines suites comportent un très grand nombre d'itérations. D'autres atteignent des "sommets" records.  

Chaque très haut "sommet" traduit l'existence d'une longue sous-suite de nombres impairs.

Ex4 :

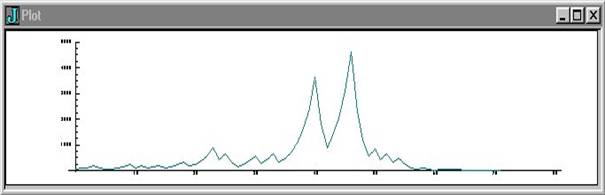
suite   55 

55 83 125 188 94 47 71 107 161 242 121 182 91 137 206 103 155 233 350 175 263 395 593 890 445 668 334 167 251 377 566 283 425 638 319 479 719 1079 1619 2429 3644 1822 911 1367 2051 3077 4616 2308 1154 577 866 433 650 325 488 244 122 61 92 46 23 35 53 80 40 20 10 5 8 4 2 1

72    4616                                           NB. 72 nombres                  maxi atteint :  4616

Ex5 :

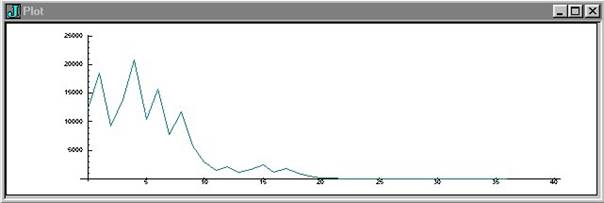
suite    12345

12345 18518 9259 13889 20834 10417 15626 7813 11720 5860 2930 1465 2198 1099 1649 2474 1237 1856 928 464 232 116 58 29 44 22 11 17 26 13 20 10 5 8 4 2 1

37  20834 NB.  nb. d'itérations : 37           maxi atteint : 20834

              Il est aisé de remarquer que les nombres de la forme  (2N+1)* 2^K  nous amèneront au nombre (2N+1), et que si N=0, c'est gagné! Cherchons à quelle condition un nombre de la forme (2N+1) sera suivi d'un nombre de la forme 2^K. Résultat facile: il faut K=2M+1 et N=2(2^2M-1)/3. 

Ceci est juste mais ne résout pas tout!

Par exemple si M=12,   N=11184810,   (2N+1)=22369621

Ex 6:

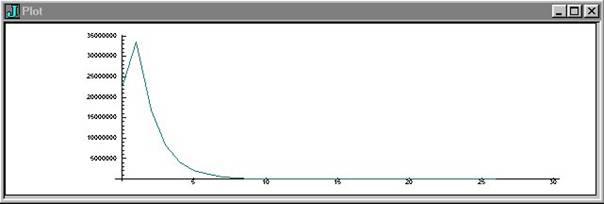
 suite  22369621

22369621 33554432 16777216 8388608 4194304 2097152 1048576 524288 262144 131072 65536 32768 16384 8192 4096 2048 1024 512 256 128 64 32 16 8 4 2 1

33554432

La conjecture est loin d'être démontrée. Intuitivement, elle ne semble pas évidente (bien que l'on n'en connaisse aucun contre-exemple). On peut imaginer 3 situations autres que la convergence vers 1 en un nombre fini d'itérations :

suite chaotique de longueur infinie (où 1 n'est jamais atteint);

suite périodique à partir d'un certain rang;

suite croissante à partir d'un certain rang;

suite "rarement" décroissante, "presque toujours" croissante….

Une "démonstration mathématique" réalisée par programme n'est pas chose aisée; tout au plus peut-on envisager actuellement:

un balayage exhaustif (et particulièrement "bestial") de tous les éléments d'un ensemble d'ordre fini (et pas "trop grand") pour démontrer un théorème d'existence ou de non existence, un dénombrement, voire un théorème d'optimisation;

un prélèvement fini (éventuellement aléatoire) dans un ensemble d'ordre infini pour tenter de démontrer un théorème d'existence.

Un exemple célèbre est la démonstration de la "conjecture des 4 couleurs" (4 couleurs sont suffisantes pour "barbouiller" toute carte géographique de telle sorte que 2 pays adjacents soient de couleurs distinctes). On a démontré, dans un premier temps, que cela revenait à démontrer une propriété de coloration des sommets d'un ensemble d'environ 20000 graphes! Il a ensuite "suffi" de programmer la vérification de cette propriété exhaustivement sur cet ensemble d'ordre 20000 (environ). Cela manque de "subtilité" mais c'est d'autant plus efficace que les ordinateurs sont plus rapides. C'est la technique du tracteur ratissant de plus en plus "vite" et de plus en plus "large"….